Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.5 - Ex. 18b
18. a. Bombeamento de azeite No Exemplo 5, quanto trabalho será necessário para bombear o azeite até 3 pés acima da borda do cone?
Passo 1
O exemplo 5 nos mostra esse recipiente.
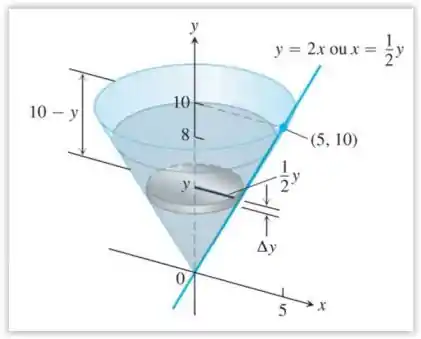
O exercício pede para calcular o trabalho para bombear o azeite, não até a borda, mas até 3 pés acima da borda.
Passo 2
Lembrando que para calcular o trabalho usamos .
Vamos descobrir quem é nosso .
Sabemos que a massa específica do azeite é , repare que isso é uma unidade de Força () dividida por uma unidade de volume, ou seja, se multiplicarmos isso pelo volume do azeite teremos unidade de força, então
E a distância será o nível do azeite até 3 pés acima do cone, ou seja
Passo 3
Agora vamos descobrir quem é nosso .
A área do disco de um cone é
Perceba que a figura nos dá que e
Então
E isso nos dá que o volume é
Nós ainda não sabemos o valor de porque o volume de água varia com o tempo, então também vai variar.
Passo 4
Agora podemos calcular a integral, como no exemplo 5, mas fazendo a devida substituição