Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.9 - Ex. 20

18) Uma quadra de basebol é um quadrado de 90 pés. Um batedor atinge a bola e corre em direção à primeira base com uma velocidade de 24 pés/s.

(a) A que taxa descreve sua distância da segunda base quando ele está a meio caminho da primeira base?

(b) A que taxa aumenta sua distância da terceira base no mesmo momento?

Passo 1

Opa, bora resolver esse problema! Em um jogo de basebol um batedor atinge a bola e corre em direção à primeira base com uma velocidade de 24 pés/s.

Temos esse esqueminha pra ajudar a gente a visualizar a quadra:

Ela é quadradinha e tem 90   f t s   de lado.

Sabendo disso, devemos responder no item (a) a que taxa descreve sua distância da segunda base quando ele está a meio caminho da primeira base!

Se chamarmos a distância do jogador à primeira base de x e a distância dele à segunda base de y , temos a seguinte situação:

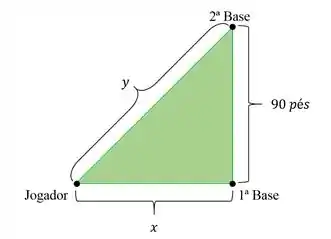
Passo 2

Logo, a relação entre x e y é:

y 2 = x 2 + 90 2

Agora, para relacionar as taxas com que x e y variam, vamos derivar implicitamente a relação entre eles em função do tempo:

2 y × y ' t = 2 x × x ' ( t )

y ' t = x × x ' t y

Quando o jogador corre em direção à primeira base, o valor de x decresce, então se ele corre nesse direção a uma velocidade de 24 pés/s, o valor de x varia a uma taxa x ' t = - 24 .

Temos que quando ele está a meio caminho da primeira base, x = 45 pés, e y é:

y 2 = 45 2 + 90 2

y = 45 5

Passo 3

Precisamos, então, substituir os valores na derivada:

y ' t = x × x ' t y

y ' t = 45 × ( - 24 ) 45 5 = - 24 5   p é s / s

Logo, por conta do valor negativo, a distância do jogador à segunda base decresce a uma taxa de 24 5   p é s / s .

Passo 4

Agora o item (b): A que taxa aumenta sua distância da terceira base no mesmo momento?

Se chamarmos a distância do jogador à terceira base de z , temos a seguinte situação:

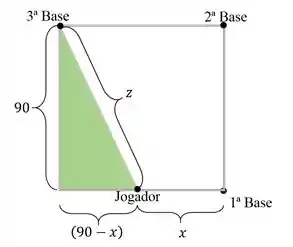
Temos então a seguinte relação:

z 2 = 90 - x 2 + 90 2

Passo 5

Agora, para relacionar as taxas com que x e z variam, vamos derivar implicitamente a relação entre eles em função do tempo:

2 z × z ' t = 2 ( 90 - x ) × ( - x ' t )

z ' t = - ( 90 - x ) × x ' t z

Para x = 45 :

z 2 = 90 - 45 2 + 90 2

z = 45 5

Temos então que nesse momento x = 45 , z = 45 5 e x ' t = - 24 , logo, z ' t é:

z ' t = - 90 - 45 × - 24 45 5 = 24 5

Logo, nesse instante a taxa com que a distância do jogador à terceira base cresce é 24 5 pés/s.

Resposta

(a) A distância do jogador à segunda base decresce a uma taxa de 24 5   p é s / s .

(b) A taxa com que a distância do jogador à terceira base cresce é 24 5 pés/s.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas pessoas começam a andar a partir do mesmo ponto. Uma vai para o leste a 3 mi/h e a outra, para o nordeste a 2 mi/h. Quão rápido está variando a distância entre as pessoas após 15 minutos?
Duas carretas, A e B, estão conectadas por uma corda de 39 pés que passa por uma polia P. O ponto Q está sobre o chão 12 pés diretamente abaixo de P e entre as carretas. A carreta A está sendo puxada
Uma piscina tem 20 pés de largura por 40 pés de comprimento, 3 pés de profundidade na parte rasa, e 9 pés na parte mais funda. Uma secção transversal está mostrada na figura. Se a piscina for preenchi
Uma câmera de televisão está posicionada a 4000 pés de uma base de lançamento de foguete. O ângulo de elevação da câmera deve variar a uma taxa qua possa focalizar o foguete. O mecanismo de foco da câ
Um cocho tem 10 pés de comprimento, e sua extremidades têm a forma de triângulos isósceles com 3 pés na base e 1 pé de altura. Se o cocho for preenchido com água a uma taxa de 12 pés/min, quão rápido