Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.7 - Ex. 4

Trace o gráfico de f x = sen ⁡ 1 2 x 2 na janela retangular 0,1 por 0 ,   0,5 e seja I = ∫ 0 1 f x d x .

  1. Use o gráfico para decidir se L 2 , R 2 , M 2 e T 2 subestimam ou superestimam I .
  2. Para qualquer valor de n , liste os números L n , R n e M n , T n e I na ordem crescente.
  3. Calcule L 5 , R 5 , M 5 e T 5 . A partir do gráfico, qual você acha que dá a melhor estimativa de I ?

Passo 1

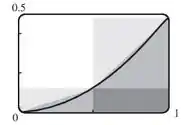
  1. Vamos observar o gráfico, já que f é crescente em 0,1 , L 2 será subestimado, já que a área do retângulo mais escuro é menor que a área abaixo da curva. R 2 é superestimado, já que f é côncavo para cima em 0,1 . M 2 é subestimado e T 2 é superestimado, já que a área abaixo dos segmentos de reta é maior que a área abaixo da curva.

    2. Passo 2

  2. Para qualquer n observado no gráfico, nós vamos ter que as aproximações a esquerda e do ponto médio são menores que I e as do trapézio e da direita são maiores:

    3. L n < M n < I < T n < R n

    Passo 3

  3. Temos o intervalo 0 ≤ x ≤ 1 , e vamos usar n = 5 , temos que ∆ x :

∆ x = b - a n = 1 - 0 5 = 1 5

Primeiro vamos achar a aproximação a esquerda L 5 , onde os x dos pontos são o ponto a esquerda em cada intervalo:

L 5 = ∑ i = 1 n f x i - 1 ∆ x = f 0 + f 0,2 + f 0,4 + f 0,6 + f 0,8 1 5 ≈ 0,1187

Passo 2

Agora vamos achar a aproximação a direita R 5 , onde os x dos pontos são o ponto a direita em cada intervalo:

R 5 = ∑ i = 1 n f x i ∆ x = f 0 , 2 + f 0,4 + f 0,6 + f 0,8 + f 1 1 5 ≈ 0 , 2 146

Passo 3

Agora vamos achar a aproximação do ponto médio M 5 , onde os x dos pontos são os pontos médios de cada intervalo:

M 5 = ∑ i = 1 n f x i - ∆ x = f 0 , 1 + f 0,3 + f 0,5 + f 0,7 + f 0,9 1 5 ≈ 0,1622

Passo 4

Para achar a aproximação pela Regra do Trapézio temos a fórmula:

T 5 = 1 2 ∆ x f 0 + 2 f 0,2 + 2 f 0,4 + 2 f 0,6 + 2 f 0,8 + f 1 ≈ 0,1666

Pelo gráfico, a melhor estimativa parece ser a do Ponto Médio

Resposta

  1. L 2 é subestimado, R 2 é superestimado, M 2 é subestimado e T 2 é superestimado
  2. L n < M n < I < T n < R n

L 5 ≈ 0,1187 , R 5 ≈ 0,2146 , M 5 ≈ 0,1622 e T 5 ≈ 0,1666 . Pelo gráfico, a melhor estimativa parece ser a do Ponto Médio

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 39 a 44, ache a área da região, tomando como medida da altura do i - é s i m o é retângulof ( m i ) , onde m i é o ponto médio do i - é s i m o é subintervalo. Sugestão: m i = 1 2 x
Nos exercícios de 39 a 44, ache a área da região, tomando como medida da altura do i - é s i m o é retângulof ( m i ) , onde m i é o ponto médio do i - é s i m o é subintervalo. Sugestão: m i = 1 2 x
Nos Exercícios de 45 a 52, uma função f e os números n , a e b são dados. Aproxime até quatro casas decimais a área da região limitada pela curva y = f ( x ) , o eixo x e as retas x = a e x = b fazend
Nos Exercícios de 45 a 52, uma função f e os números n , a e b são dados. Aproxime até quatro casas decimais a área da região limitada pela curva y = f ( x ) , o eixo x e as retas x = a e x = b fazend
Nos Exercícios de 45 a 52, uma função f e os números n , a e b são dados. Aproxime até quatro casas decimais a área da região limitada pela curva y = f ( x ) , o eixo x e as retas x = a e x = b fazend