Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.10 - Ex. 20
Um cocho tem pés de comprimento, e sua extremidades têm a forma de triângulos isósceles com pés na base e pé de altura. Se o cocho for preenchido com água a uma taxa de , quão rápido estará se elevando o nível da água quando estiver polegadas de profundidade?
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você??Vamos analisar o que nosso probleminha está falando.
Bom, ele nos diz que temos um cocho de pés de comprimento, a lateral tem base igual a 3 pés e altura igual a 1 pé e é um triângulo isósceles.
Depois, ele nos diz que está enchendo tudo com água até polegadas de profundidade a uma taxa de , e nos pede a velocidade que o cocho está enchendo.
Tem ideia de como fazemos isso?
Caso você não saiba, um cocho é um recipiente grande que é usado para colocar comida/água para bois.
Para encontrar a taxa de elevação de nível de água quando a altura da água estiver em polegadas, vamos primeiro determinar o volume do cocho e tentar escrever esse volume como uma função da altura. Assim, como estamos tratando de taxas de variação, podemos derivar o volume em relação ao tempo, que nos resulta no valor de (dado no enunciado) e a partir da taxa relacionada à altura da água, encontrar a taxa de variação da água.
Entendeu alguma coisa? Bora ver na prática!
Passo 2
Primeiro vamos desenhar nosso cocho com as informações dadas no enunciado
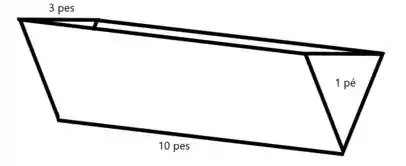
O volume desse cocho é a area lateral do triangulo multiplicado pelo seu comprimento
Nosso primeiro passo vai ser fazer a semelhança de triângulos para definir a base em função da altura .
Com essa relação, sabendo que é constante, independente da altura, temos que o volume é:
Show? Essa é nossa função volume em relação à altura .
Passo 3
Com esse volume, vamos derivar os dois lados em relação a , pois a taxa de enchimento de água dada no enunciado é em
é uma função do tempo pois ele representa a altura da água com o tempo, então derivamos aplicando a regra da cadeia.
Substituindo em , temos
Esse valor é justamente o valor que estamos procurando, que é a taxa de variação da altura. Então vamos isolá-lo
Queremos a taxa de variação da altura, quando ... convertendo para , temos que , logo .
Além disso, a taxa de enchimento do cocho é de , ou seja
É isso! O que achou? Responde Aí!