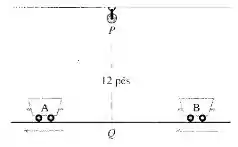
Duas carretas, A e B, estão conectadas por uma corda de 39 pés que passa por uma polia P. O ponto Q está sobre o chão 12 pés diretamente abaixo de P e entre as carretas. A carreta A está sendo puxada afastando-se de Q a uma velocidade de 2 pés/s. Quão rápido está se movendo a carreta B em direção a Q no instante em que A está a 5 pés de Q?
Passo 1
Opa, bora lá! Temos o seguinte esqueminha:
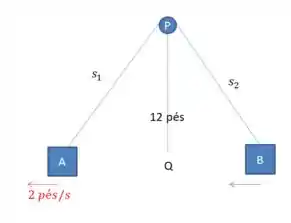
Onde se move para a esquerda com , temos que a altura da polia até o chão é de e que a corda tem no total , logo:
Queremos encontrar com que velocidade se move para a esquerda, quando ele está está a uma distância de de pés, ou seja, nesse instante:
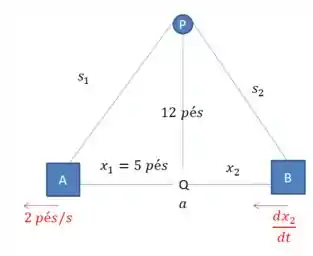
Perceba que a velocidade com que se aproxima de é a nossa derivada de , portanto, o que queremos encontrar nessa questão é:
E para isso, vamos usar os triângulos formados e a famosa regra de Pitágoras.
Passo 2
Podemos começar encontrando o valor de , e para isso, vamos aplicar Pitágoras no triângulo retângulo menor que está a esquerda, onde teremos:
Logo,
Da mesma forma, podemos aplicar Pitágoras no triângulo retângulo menor que está a direita, onde teremos:
E sabemos que, o comprimento total da corda é , logo:
Portanto,
Como queremos encontrar e temos , então temos um bom indicativo de que é uma boa solução tentar derivar a expressão acima.
Passo 3
Derivando a seguinte expressão com relação ao tempo, teremos:
Aqui temos uma regra da cadeia com essa raíz, que precisamos tomar cuidado, além de não esquecer de que estamos derivando em e nossa variável é e ,logo, tem que multiplicar por e no final:
Simplificando:
Sabemos o valor de , e positivo, pois essa velocidade de fato faz com que o aumente com o tempo. E também sabemos que é igual a .
Agora precisamos encontrar o valor de no instante dado.
Passo 4
Só trazendo nossa figura de novo.
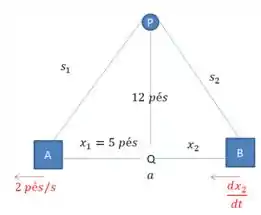
Olhando o triângulo da esquerda, podemos dizer por Pitágoras que:
Com essa informação, podemos agora encontrar o valor de , afinal sabemos que a corda no total tem .
E para finalizar, podemos encontrar o valor de , aplicando Pitágoras no triângulo retângulo menor que está a direita, onde teremos:
Passo 5
Para finalizar é só substituir:
Resolvendo...
E resolvendo para , obtemos:
E por fim,