Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.4 - Ex. 67
Considere
é derivável em 1? Esboce os gráficos de .
Passo 1
Opa, vamos fazer essa questão! O enunciado nos dá:
E pergunta se existe! Para isso a gente vai calcular a derivada de em usando a definição de derivada:
Só que aqui vamos aproximar de zero pela direita e pela esquerda. Se os limites laterais forem iguais, então a nossa função é derivável em , caso contrário ela não é!
Bora colocar a mão na massa!
Passo 2
À esquerda de temos:
Então:
Calculando:
Para :
Agora pela direita de :
Temos que:
Portanto:
Como os limites laterais são diferentes, já podemos concluir que a função não é contínua em , logo não é diferenciável nesse ponto também.
Passo 3
Vemos isso claramente nos gráficos:
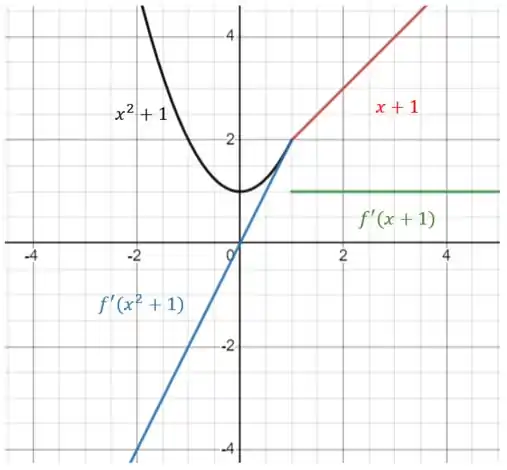
Resposta
não é diferenciável em .
Exercícios de Livros Relacionados
Determine os valores de a e b que tornam a seguinte função derivável para todos os valores de x . f x = a x + b , b x 2 - 3 , s ex- 1 s ex ≤ - 1
Determine o valor de a que torna a seguinte função derivável para todos os valores de x . g x = a x , x 2 - 3 x , s ex0 s ex ≥ 0
Seja f x uma função que satisfaz f x ≤ x 2 para - 1 x1 Mostre que f ( x ) é derivável em x =0 e determine f ' ( 0 ) . Mostre que f x = x 2 ∙s e n1 x , x ≠ 0 0 , x = 0 é derivável em x=0 e determine f
Em que pontos do domínio a função parece ser derivável? contínua, mas não derivável? nem contínua, nem derivável?
Em que pontos do domínio a função parece ser derivável? contínua, mas não derivável? nem contínua, nem derivável?