Exercícios de Taxa Relacionada - Lista de Exercícios Resolvida
Questão 1
A voltagem (volts), a corrente (amperes) e a resistência (ohms) de um circuito elétrico (veja a seguir) estão relacionadas entre si pela equação . Suponha que esteja aumentando a uma taxa de , enquanto está diminuindo a uma taxa de . Representaremos o tempo em segundos.
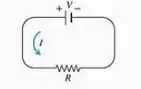
Qual é o valor de ?
Qual é o valor de ?
Qual equação relaciona , e ?
Encontre a taxa com a qual está variando quando e . está aumentando ou diminuindo?
Ver solução completaQuestão 2
Sejam e funções deriváveis de e seja a distância entre os pontos e no plano .
Como está relacionada a se é constante?
Como está relacionada a e se nem nem são constantes?
Como está relacionada a se 𝑠 é constante?
Ver solução completaQuestão 3
Se a água estiver sendo drenada de uma piscina e litros for o volume de água na piscina min após começar o escoamento, onde
,
ache:
A taxa média segundo a qual a água deixa a piscina durante os primeiros 5 min.
Quão rápido a água está fluindo da piscina após o início do escoamento.
Ver solução completaQuestão 4
Em cada item a seguir, encontre os intervalos de crescimento e decrescimento da função dada. Em seguida, determine seus pontos de máximo e mínimo locais (se existirem).
(c)
Ver solução completaQuestão 5
Os comprimentos dos lados de um retângulo variam com o tempo. Sabe-se que a taxa de variação do maior lado é o dobro da taxa de variação do menor lado.
- Se a taxa de variação da área é , qual a taxa de variação do menor lado?
- Se o comprimento da diagonal cresce a , qual a taxa de variação do menor lado?
Dados para (a) e (b): no instante em que o maior lado mede 5cm, o menor mede 3cm.
Ver solução completaQuestão 6
Os comprimentos dos lados de um retângulo variam com o tempo. Sabe-se que a taxa de variação do maior lado é o dobro da taxa de variação do menor lado.
- Se a taxa de variação da área é , qual a taxa de variação do menor lado?
- Se o comprimento da diagonal cresce a , qual a taxa de variação do menor lado?
Dados para (a) e (b): no instante em que o maior lado mede 5cm, o menor mede 3cm.
Ver solução completaQuestão 7
Seja definida implicitamente pela equação . Encontre o coeficiente angular da reta normal ao gráfico da função no ponto .
Ver solução completaQuestão 8
Uma partícula se move sobre uma linha reta de acordo com a equação , sendo a distância (em metros) da partícula ao seu ponto de partida, após decorridos segundos da partida.
(a) Calcule a velocidade média da partícula de até .
(b) Calcule a velocidade instantânea da partícula quando
Ver solução completaQuestão 9
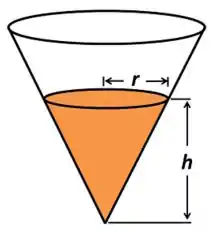
Questão 1.4 - Um recipiente em formato cônico é construído com altura fixa de . A circunferência da base mede com um possível erro de . Dê uma estimativa para o erro no cálculo do volume da peça (use nas contas a aproximação ).
Ver solução completaQuestão 10
No instante horas um veículo está quilômetros à leste de um ponto de referência na estrada.
(a) Qual a velocidade no instante e qual é o sentido do movimento em relação ao ponto de referência?
(b) Onde está o veículo quando a velocidade é zero?
Ver solução completaQuestão 11
Na figura abaixo, o segmento mede e é tangente à circunferência de raio no ponto . O ponto é determinado pela interseção da circunferência com o segmento . O ponto inicia um movimento de descida, pela vertical, em direção ao ponto a uma taxa constante de .
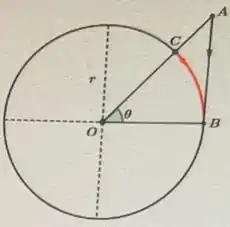
A taxa com que se movimenta o ponto , ao longo do arco , depois de segundos do ponto ter iniciado o seu movimento é
:
:
:
:
:
Ver solução completaQuestão 12
Um caminhão descarrega areia a uma taxa de de tal forma que a areiai descarregada tem um formato de cone em que a altura é igual ao diâmetro da base. Determine a taxa de crescimento da altura da pilha quando a altura for igual a .
Ver solução completaQuestão 13
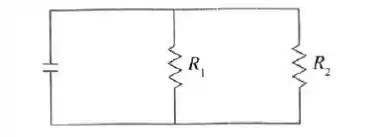
Se dois resistores com resistências e estão conectados em paralelo, como na figura, então a resistência total , medida em ohms (, é dada por
Se e estão crescendo a taxas de e , respectivamente, quão rápido estará variando quando e ?
Questão 14
Dois lados paralelos de um retângulo aumentam a uma velocidade de , enquanto os outros dois diminuem de modo que a área desse retângulo permanece constante e igual a . Determine a taxa de variação do perímetro desse retângulo quando o comprimento dos lados que aumentam é ; .
Ver solução completaQuestão 15
Um barco deixa as docas às e navega para o sul a uma velocidade de . Um outro barco está se dirigindo para leste a uma velocidade de e atinge a mesma doca às .
Determine a velocidade de afastamento entre os dois barcos às.
Ver solução completaQuestão 16
Um avião está voando com velocidade constante a uma altitude de paralelamente ao solo.
Em um dado instante, um observador situado no solo observa que o ângulo de elevação do avião é de e está aumentando a uma taxa de . Calcule a velocidade do avião.
Ver solução completaQuestão 17
O raio de um cilindro circular reto aumenta com velocidade constante. Sua altura é uma função
afim do raio e aumenta 3 vezes mais rápido do que este, de modo que quando o raio mede , a altura mede . No instante em que o raio mede , o volume aumenta a uma razão de . Determine a taxa de variação do volume no instante em que o raio do cilindro mede .
Ver solução completaQuestão 18
Um balão esférico está sendo inflado a uma taxa de . Determine a taxa de variação
da sua superfície no instante em que o diâmetro desse balão é igual a .
Ver solução completaQuestão 19
Um reservatório cônico de de profundidade e de diâmetro está recebendo água na razão de . Determine:
b) A taxa de variação da área da superfície da água quando esta estiver a ;
Ver solução completaQuestão 20
Uma pipa, situada acima do solo, move-se horizontalmente a . Sabendo que a linha se encontra esticada, determine a taxa de variação do ângulo que essa linha faz com a horizontal no instante em que o comprimento da mesma for de .
Ver solução completaQuestão 21
Considere o ponto deslocando-se sobre o gráfico
, para ,
Onde e são medidos em centímetros. Denotemos por o ponto dado pela interseção do eixo com a reta tangente ao gráfico de no ponto . Sabendo que a coordenada do ponto varia a uma taxa constante de , determine com que taxa estará variando a coordenada do ponto no instante em que as coordenadas do ponto forem .
Ver solução completa
Questão 22
Os ponteiros de um relógio mede 4 cm e 8 cm e movem-se, cada um com sua velocidade, que é constante. Quando o relógio marca exatamente duas horas, a distância entre as pontas dos ponteiros está diminuindo a uma taxa de:
Ver solução completaQuestão 23
Um projétil é lançado verticalmente para cima e segundos após o lançamento está metros do solo, onde . Calcule:
- A altura máxima atingida pelo projétil
Questão 24
Uma partícula se move sobre uma linha reta de acordo com a equação , sendo a distância (em metros) da partícula ao seu ponto de partida, após decorridos segundos da partida.
- Calcule a velocidade média da partícula de até
Questão 25
Um projétil é lançado verticalmente para cima e segundos após o lançamento está metros do solo, onde . Calcule:
- A velocidade do projétil segundos após o lançamento
Questão 26
No instante horas um veículo está quilômetros à leste de um ponto de referência na estrada
- Qual a velocidade no instante e qual é o sentido do movimento em relação ao ponto de referência?
Questão 27
Uma partícula se move sobre uma linha reta de acordo com a equação , sendo a distância (em metros) da partícula ao seu ponto de partida, após decorridos segundos da partida.
b) Calcule a velocidade instantânea da partícula quando
Ver solução completaQuestão 28
Uma escada de está encostada numa parede. Se a extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de , com que velocidade a extremidade superior estará descendo no instante em que a inferior estiver a da parede?
Ver solução completaQuestão 29
Um ponto move-se sobre a semicircunferência . Suponha . Determine o ponto da curva em que a velocidade de seja o dobro da velocidade de .
Ver solução completaQuestão 31
O raio de luz de um farol, que está situado a de uma praia reta, faz (rotações por minuto). Considere a altura do farol desprezível em relação a sua distância até à praia. Ache a velocidade da extremidade do raio de luz, no longo da praia, quando ele faz um ângulo de com a linha da praia.
Ver solução completaQuestão 32
Num determinado instante, um controlador de tráfego aéreo vê dois aviões na mesma altura voando a velocidades constantes, em trajetórias ortogonais que se cruzam num ponto (veja figura). Neste instante, um dos aviões está a milhas do ponto e se aproxima de à milhas por hora, enquanto o outro está a milhas do ponto e se movendo à milhas por hora, também em direção ao ponto .
- Antes do ponto , a distância entre os aviões está diminuindo? A que taxa?
Questão 33
Uma câmara de televisão no nível do solo está filmando a subida de um ônibus espacial que está subindo verticalmente de acordo com a equação , sendo a altura e o tempo. A câmara está a do local de lançamento. Encontre a taxa de variação da distância entre a câmara e a base do ônibus espacial, após o lançamento (suponha que a câmara e a base do ônibus estão no mesmo nível no tempo).
Ver solução completaQuestão 34
Um ponto, move-se ao longo da elipse . A abscissa x está variando com velocidade
Mostre que
Ver solução completaQuestão 35
Um homem se encontra em um barco a remo a 3km da costa e deseja chegar a uma cidade litorânea que está a 6 km em linha reta do ponto (na costa) mais próximo do barco. Ele rema a 4 km/h e caminha a 5 km/h. Onde ele deve aportar para chegar à cidade do no menor tempo possível.
Ver solução completaQuestão 36
Um cilindro circular reto é obtido girando-se um retângulo de diagonal constante e igual a em torno de um dos seus lados. Determine a taxa de variação do volume do cilindro no instante que a altura do cilindro é e está aumentando à razão de .
Ver solução completaQuestão 37
No estudo de ecossistemas, o modelo predador-presa é muitas vezes usado para estudar a interação entre espécies. Seja o número de tigres de uma região no instante de tempo (medido em anos) e seja o número de antílopes na mesma região no instante . A interação entre essas duas espécies é modelada pelas equações
e ,
Em que e são constantes.
- Como caracterizar matematicamente a afirmação de que o número de indivíduos das duas espécies é constante ao longo do tempo?
- Como caracterizar matematicamente a extinção dos antílopes?
- Considere . Sabendo que as espécies estão convivendo em equilíbrio (isto é, o número de indivíduos é constante ao longo do tempo) e que não estão extintas, determine o número de indivíduos de cada espécie.
Questão 38
É muito comum falarmos em taxa de crescimento usando porcentagens: por exemplo, a população cresce 1% ao ano. Essa medida é uma medida relativa comparada ao seu valor prévio: a população do ano seguinte é 1% maior que a população do ano atual. Apesar de não parecer, essa afirmação pode ser traduzida matematicamente usando a noção de taxa de variação média: se P(t) é a população no ano t, então essa afirmação pode ser escrita como
O denominador da fração do lado esquerdo é , mas colocamos na forma de para ilustrar o quociente que representa a taxa de variação média. E se essa informação da taxa de crescimento relativa não for “média”, mas sim instantânea? Neste caso, o lado esquerdo da igualdade é trocado por e ficamos com
- Mostre que , em que é a população no instante de tempo , é solução da equação acima.
- Mostre que , em que é a população no instante de tempo , é solução da equação .
- Justifique a afirmação: “Em uma população modelada pela função , em que é medido em anos, a taxa de crescimento anual é .”
- Determine a taxa de crescimento anual de uma população que cresce proporcionalmente ao seu tamanho e que, em anos, saltou de bilhões para bilhões de habitantes
Questão 39
Está vazando água de um tanque cônico invertido a uma taxa de . Ao mesmo tempo, está sendo bombeada água para dentro do tanque a uma taxa constante. O tanque tem de altura e o diâmetro no topo é de . Se o nível da água estiver subindo a uma taxa de quando a altura da água for , encontre a taxa segundo a qual a água está sendo bombeada para dentro do tanque.
Ver solução completaQuestão 40
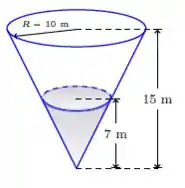
Enche-se um reservatório, cuja forma é a de um cone circular reto, de água a uma taxa de . O vértice está a do topo e o raio é de . Com que velocidade o nível h da água está subindo no instante em que .
Questão 41
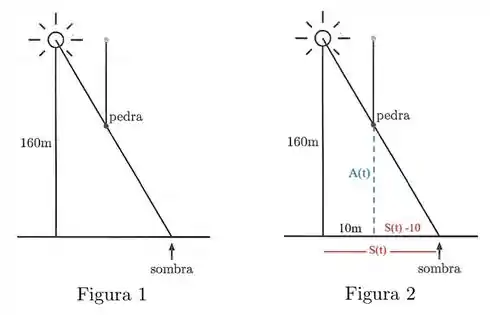
Uma pedra é jogada de uma altura de . Um foco de luz está colocado também a de altura, a uma distância de da posição inicial da pedra. A altura da pedra após segundos é metros. Com que velocidade se moverá a sombra da pedra sobre o chão segundos após a pedra ser jogada?
Questão 42
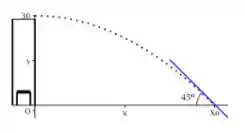
Um aluno foi desafiado a chutar uma bola do alto de um prédio com de altura, de modo a atingir o solo com a inclinação de . Sabendo-se que a bola descreve uma trajetória parabólica dada pela equação , onde é a distância percorrida horizontalmente pela bola, é a altura da bola e é a velocidade horizontal aplicada pelo aluno no momento do lançamento, determine o valor de para que o aluno vença o desafio.
Questão 43
Questão 3:
Considere o triângulo retângulo com catetos e . Sabemos que aumenta a uma taxa de , e que a área do triângulo permanece sempre igual a . A que taxa varia a hipotenusa do triângulo, quando ?
Ver solução completaQuestão 44
A lei de Boyle estabelece que quando uma amostra de gás é comprimida a uma temperatura constante, o produto da pressão e do volume permanece constante:
Encontre a taxa de variação do volume em relação a pressão.
Ver solução completaQuestão 45
A lei de Boyle estabelece que quando uma amostra de gás é comprimida a uma temperatura constante, o produto da pressão e do volume permanece constante:
Uma amostra de gás está em um recipiente a baixa pressão e é regularmente comprimida a temperatura constante por 10 min. O Volume decresce mais rapidamente no início ou final dos 10 minutos. Explique.
Ver solução completaQuestão 46
Dois carros iniciam o movimento de um mesmo ponto. Um viaja para o sul a 60 mi/h, e o outro para o oeste a 25 mi/h. A que taxa está crescendo a distância entre os carros duas horas depois?
Ver solução completaQuestão 47
5) Um caminhão despeja cimento sobre o solo, que se acumula em um monte da forma de um cone, cuja altura é igual ao raio da base. Se o volume de cimento aumenta a uma taxa de , a que razão aumenta a área da base do monte formado pelo cimento, quando sua altura é de ?
Ver solução completaQuestão 48
Um projétil é lançado verticalmente para cima e segundos após o lançamento está metros do solo, onde . Calcule:
- O tempo necessário para o projétil atingir a altura máxima
Questão 49
No instante horas um veículo está quilômetros à leste de um ponto de referência na estrada
- Onde está o veículo quando a velocidade é zero?
Questão 50
Um reservatório retangular de largura tem um painel interno que desliza com velocidade de afastamento .
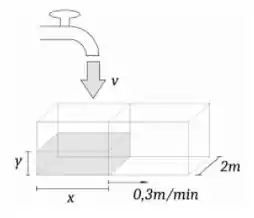
Sabendo-se que num determinado momento, o volume de água do reservatório da esquerda é e está crescendo à taxa de , determine se o nível de água está subindo ou descendo e com que velocidade nos seguintes casos:
a. No instante dado, o reservatório da esquerda tem comprimento
b. O reservatório da esquerda tem comprimento , naquele momento
Ver solução completaQuestão 51
Um farol, situado a uma distância de de uma muralha, completa voltas por minuto. Quando o facho de luz ilumina um ponto da muralha, situado a do farol, a velocidade com que o ponto de luz varre a muralha é de:
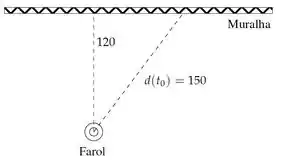
Questão 52
Um farol, situado a uma distância de de uma muralha, completa voltas por minuto. Quando o facho de luz ilumina um ponto da muralha, situado a do farol, a velocidade com que o ponto de luz varre a muralha é de:
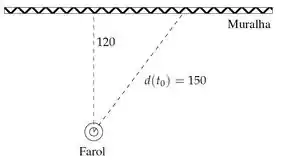
Questão 53
Um tanque tem de comprimento e sua seção transversal é sempre um triângulo equilátero, conforme a figura abaixo. Está sendo bombeada água para o interior do tanque a uma taxa de . Com que velocidade o nível da água estará subindo quando o conteúdo de água no tanque estiver com de profundidade?
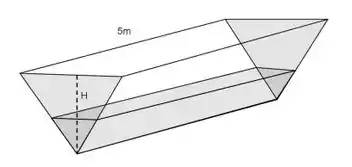
Questão 54
Em uma fazenda de psicultura, uma população de peixes é colocada dentro de um lago e colhido regularmente. Um modelo para variação da população é dada pela equação:
Em que é a taxa de nascimento dos peixes, é a população máxima que o pequeno lago pode manter (capacidade de suporte) e é a porcentagem da população que é colhida.
O que acontece se é elevado a 5%?
Ver solução completaQuestão 55
O lado de um cubo é medido com um erro máximo possível de 2%. Use diferenciais para estimar o percentagem de erro máximo no volume computado.
Ver solução completaQuestão 56
Se uma bola de neve derrete de tal forma que sua área de superfície decresce a uma taxa de 1 cm²/min, encontre a taxa segundo a qual o diâmetro decresce quando o diâmetro é 10 cm.
Ver solução completaQuestão 57
Em uma fazenda de psicultura, uma população de peixes é colocada dentro de um lago e colhido regularmente. Um modelo para variação da população é dada pela equação:
Em que é a taxa de nascimento dos peixes, é a população máxima que o pequeno lago pode manter (capacidade de suporte) e é a porcentagem da população que é colhida.
Se o pequeno lago pode manter 1000 peixes a taxa de nascimento é 5% e a taxa de colheita é de 4%, encontre o nível estável da população.
Ver solução completaQuestão 58
Se uma bola de neve derrete de tal forma que sua área de superfície decresce a uma taxa de 1 cm²/min, encontre a taxa segundo a qual o diâmetro decresce quando o diâmetro é 10 cm.
Ver solução completaQuestão 59
3. A areia cai de uma esteira transportadora a uma taxa de no topo de uma monte cônico. A altura do monte sempre tem do diâmetro da base. A que taxa irá variar o raio da base quando o monte tiver de altura?
Ver solução completaQuestão 60
Uma câmera de televisão no nível do solo está filmando a subida de um ônibus espacial que está subindo verticalmente de acordo com a equação sendo s a altura e t o tempo. A câmera está a 600 m do local de lançamento. Encontre a taxa de variação da distância entre a câmera e a base do ônibus espacial, 10 segundos após o lançamento (suponha que a câmera e a base do ônibus estão no mesmo nível no tempo t = 0).
Ver solução completaQuestão 61
Considere um cubo inscrito numa esfera. Conforme o lado do cubo aumenta, a esfera também aumenta, de forma que o primeiro esteja sempre inscrito na segunda. Sabendo que o lado do cubo varia a uma taxa de , qual a taxa de variação do volume da esfera quando o cubo alcançar ?
Ver solução completaQuestão 62
Um ponto move-se ao longo da elipse . A abcissa está variando a uma velocidade . Mostre que
Questão 64
Um balão esférico esta sendo esvaziado a uma taxa de . Encontre a taxa de decrescimento do raio do balão quando o diâmetro for igual a .
Ver solução completaQuestão 65
Considere a parábola na figura abaixo, onde a reta é tangente à parábola no primeiro quadrante em cada ponto . Sabendo que a taxa de variação da abscissa de (coordenada ) é de , determine a taxa de variação do lado do triângulo , quando o ponto de tangência é .
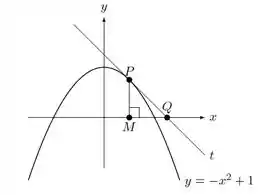
Questão 66
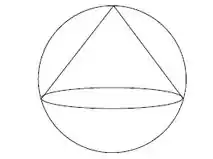
Um cone está inscrito em uma esfera conforme mostra figura abaixo. Se o raio da esfera está aumentando a uma taxa de e a altura do cone está aumentando a uma taxa de , com que taxa está aumentando o volume do cone no instante em que o raio da esfera mede e a altura do cone mede .
Questão 67
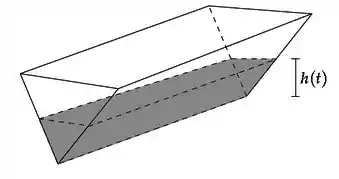
Uma mangueira está enchendo um tanque com água. O tanque tem o formato de um prisma de comprimento cuja base é um triângulo equilátero (ver figura abaixo). Sabendo que a vazão é constante e igual a , determine a taxa de variação da altura da água, no instante em que ela é .
Questão 68
Uma pedra caiu dentro de um lago, produzindo uma ondulação circular que cresce a uma velocidade radial de 60 m/s. Encontre a taxa segundo conforme a qual a área dentro do círculo está crescendo depois de a) 1s b) 3s c) 5s. O que você pode concluir
Ver solução completaQuestão 69
3. A posição (em metros) de um objeto em função do tempo (em segundos) é dada por . Determine a posição e a velocidade do objeto no instante .
Ver solução completaQuestão 70
Num determinado instante, um controlador de tráfego aéreo vê dois aviões na mesma altura voando a velocidades constantes, em trajetórias ortogonais que se cruzam num ponto (veja figura). Neste instante, um dos aviões está a milhas do ponto e se aproxima de à milhas por hora, enquanto o outro está a milhas do ponto e se movendo à milhas por hora, também em direção ao ponto .
b) Os aviões correm risco de choque? Em caso afirmativo, quanto tempo o controlador tem
para fazer com que um dos aviões mude a sua trajetória?
Ver solução completaQuestão 71
A produção mensal de papel de uma indústria é dada pela expressão , onde é o número de meses contado a partir de uma certa data e é a quantidade de papel em toneladas. Apresente no máximo duas casas decimais em seus resultados.
Determine a taxa de variação média de produção entre o segundo e o quinto mês.
Ver solução completaQuestão 72
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função
Em que é medido em horas. No instante a população é de 20 células e está crescendo a uma taxa de . Encontre os valores de e . De acordo com este modelo, o que ocorre com a população de levedura depois de muito tempo?
Ver solução completaQuestão 73
A produção mensal de papel de uma indústria é dada pela expressão , onde é o número de meses contado a partir de uma certa data e é a quantidade de papel em toneladas. Apresente no máximo duas casas decimais em seus resultados.
Calcule a taxa de variação instantânea em .
Dica: .
Ver solução completaQuestão 74
Um reservatório de água no formato de um cone circular reto (vértice em baixo) está sendo enchido a uma taxa de . O vértice está a metros do topo e o raio do topo é de metros. Com que velocidade o nível da água está subindo no instante em que ( medindo de baixo para cima)?
Ver solução completaQuestão 75
Cascalho está caindo e formando uma pilha cônica que aumenta a uma taxa de 3m³/min, de modo que o raio do cone é sempre igual a sua altura. Encontre a taxa de variação da altura da pilha quando a altura é de 3m.
Ver solução completaQuestão 76
A posição de uma partícula sobre uma linha reta graduada em metros no instante segundos é dada por
- Determine
- Determine
- Em quais instantes a partícula está em repouso?
- Quando a partícula está se movendo para frente? E quando está se movendo para trás?
- Qual é o deslocamento da partícula entre os instantes e ?
- Qual é a distância percorrida pela partícula entre os instantes 0 e 5s?
- Para que valores de tem-se Para quais valores de tem-se Para quais valores de tem-se
- Quando a partícula está acelerando ou freando?
Questão 77
Dois carros iniciam o movimento partindo de um mesmo ponto. Um viaja para o sul a e o outro para oeste a . A que taxa está crescendo a distância entre os carros duas horas depois?
Um carro A está se movimentando para o oeste a 90km/h e o carro B está se movimentando para o norte a 100 km/h. Ambos vão em direção à interseção de duas estradas. A que taxas os carros se aproximam um do outro quando o carro A está a 60 m e o carro B está a 80 m da interseção?
Ver solução completaQuestão 78
2) Uma pedra jogada em um lago emite ondas circulares, de modo que a área da região englobada pela onda cresce à taxa de Com que rapizes estará crescendo o raio da onda no instante que este for ? Justifique sua resposta
Ver solução completaQuestão 79
Uma mulher está andando com uma velocidade de ao longo do diâmetro de um pátio
circular. Uma luz, situada no extremo de outro diâmetro perpendicular ao seu caminho, projeta sua sombra sobre a parede circular do pátio. Determine a velocidade com a qual a sombra da mulher estará se movendo ao longo da parede quando a mulher tiver percorrido do diâmetro do pátio.
Ver solução completaQuestão 80
Cada lado de um quadrado está aumentando a uma taxa de . A que taxa a área do quadrado está aumentando quando a área do quadrado é ?
Ver solução completaQuestão 81
7. Uma escada de está encostada em uma parede. Se a extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de , com que velocidade a extremidade superior estará descendo no instante em que a inferior estiver a da parede?
Ver solução completaQuestão 82
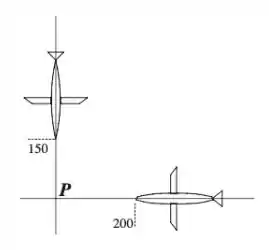
Num determinado instante, um controlador de tráfego aéreo vê dois aviões na mesma altura voando a velocidades constantes, em trajetórias ortogonais que se cruzam num ponto P como descrito na figura ao lado. Neste instante, um dos aviões está a 150 milhas do ponto P e se aproxima de P a 450 milhas por hora, enquanto o outro está a 200 milhas do ponto P e se movendo a 600 milhas por hora, também em direção ao ponto P.
- Antes do ponto P, a distância entre os aviões está diminuindo? A que taxa?
- Os aviões correm risco de choque? Em caso afirmativo, quanto tempo o controlador tem para fazer com que um avião mude a sua trajetória?
Questão 83
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função
Em que é medido em horas. No instante a população é de 20 células e está crescendo a uma taxa de . Encontre os valores de e . De acordo com este modelo, o que ocorre com a população de levedura depois de muito tempo?
Ver solução completaQuestão 84
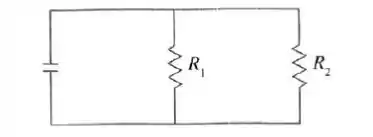
Se dois resistores com resistências e estão conectados em paralelo, como na figura, então a resistência total , medida em ohms (, é dada por
Se e estão crescendo a taxas de e , respectivamente, quão rápido estará variando quando e ?
Questão 85
Um funil cônico têm diâmetro de na parte superior e altura de . Se o funil for alimentado à taxa de e tem uma vazão de , determine quão rapidamente está subindo o nível de água quando esse nível for de .
Ver solução completaQuestão 86
Um ponto move-se sobre o gráfico de , de tal modo que sua abscissa varia a uma velocidade de . Qual a velocidade de no instante em que é igual a ?
Ver solução completaQuestão 87
2. Um copo de papel tem a forma de um cone de de altura e de raio (no topo). Se for colocada água dentro do copo a uma taxa de , com que rapidez o nível da água se elevará quandro ela tiver de profundidade?
Ver solução completaQuestão 88
2. A área de um círculo aumenta a uma taxa constante de . Calcule a taxa de variação da sua circunferência quando o raio é igual a .
Ver solução completaQuestão 89
8. Uma partícula se desloca ao longo da parábola no primeiro quadrante de modo que sua coordenada (medida em metro) aumente a uma velocidade constante de . Qual é a derivada em relação ao tempo do ângulo de inclinação da reta que liga a partícula à origem quando .
Ver solução completaQuestão 90
Um carro, vindo do norte, aproxima-se de um cruzamento em ângulo reto a uma velocidade de . Ao mesmo tempo, um outro carro, que se situa à leste do cruzamento, afasta-se a uma velocidade de . Determine a taxa de variação da distância entre os dois carros no instante em que o primeiro está a do cruzamento e o segundo está a do cruzamento. Qual a interpretação física do sinal do resultado encontrado?
Ver solução completaQuestão 91
Um objeto circular aumenta de tamanho de alguma forma desconhecida. Entretanto, é sabido que quando o raio é igual a , a taxa de variação do raio é igual a . Encontre a taxa de variação da área quando o raio é igual a .
Ver solução completaQuestão 92
Sejam , com e um ponto sobre o gráfico de . Considere a reta tangente ao gráfico de no ponto e o ponto em que intercepta o eixo .
Determine, em termos da abscissa de , a abscissa do ponto .
Suponha que o ponto esteja sobre o gráfico de e que no instante em que sua abscissa esteja se deslocando a uma taxa de variação de unidades por segundo.
Determine a taxa de variação da abscissa do ponto nesse instante.
Seja o ângulo que a reta forma com o eixo . Determine a taxa de variação de nesse mesmo instante.
Ver solução completaQuestão 93
Um balão esférico está sendo enchido a uma taxa de . Encontre a taxa de crescimento do raio do balão quando o diâmetro for igual a .
Lembre que o volume da esfera de raio é igual a
Ver solução completaQuestão 94
Um biólogo está em uma ponte sobre um rio e está inspecionando o rio com o auxílio de um drone. O drone mantém uma altura constante de com relação à ponte. O biólogo mantém o drone sobrevoando um trecho do rio em linha reta a uma velocidade constante de . Qual a taxa de variação da distância entre o biólogo e o drone quando a distância entre os dois for de ?
Ver solução completaQuestão 95
Um petroleiro se rompeu e uma mancha de óleo está se espalhando na superfície do mar. Sabe-se que a mancha de óleo tem superfície plana e circular e que o raio da mancha está crescendo a uma taxa constante de . Qual a taxa de crescimento da área da mancha quando o raio da mancha for igual a ?
Ver solução completaQuestão 96
Um economista anunciou que os juros estão crescendo, mas a uma taxa decrescente. Interprete esta afirmação em termos de derivada.
Ver solução completaQuestão 97
Um quadro com de altura está colocado numa parede vertical, sendo que sua base está a acima do nível dos olhos de um observador. Se o observador está se aproximando da parede a uma velocidade de , determine a taxa de variação da medida do ângulo de visão da pintura no instante em que o observador estiver a da parede.
Ver solução completaQuestão 98
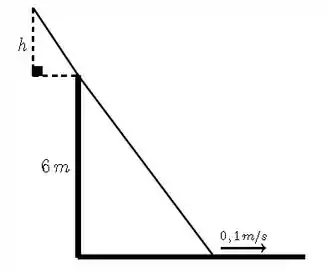
Uma escada de de comprimento está apoiada em um muro de de altura, conforme
representado na figura. A base da escada desliza pelo chão, afastando-se do muro, com velocidade constante de . Determinar a taxa de variação instantânea da altura , indicada na figura, no instante em que a base da escada está a uma distância de do muro.
Questão 99
Um fabricante produz peças de tecido. O custo, em reais, da produção de metros de um certo tecido é .
- Qual é o significado de Qual é a unidade de
- O que significa dizer que
Questão 100
Um corredor corre em uma trajetória circular de raio a uma velocidade constante de . Um outro indivíduo está parado a uma distância de do centro da pista. Qual a taxa de variação da distância entre os dois quando esta distância for de ?
Lembre que o comprimento do arco de um setor circular de ângulo (em radianos) de uma circunferência de raio é igual a .
Ver solução completaQuestão 101
Um economista anunciou que os juros estão crescendo, mas a uma taxa decrescente. Interprete esta afirmação em termos de derivada.
Ver solução completaQuestão 102
Uma escada com de comprimento está apoiada em uma parede vertical. Se a base da
escada desliza afastando-se da parede a uma taxa de , quão rápido o topo da escada
está escorregando para baixo na parede quando a base da escada está a da parede
(medido no chão)?
Ver solução completaQuestão 103
Um tanque de água possui o formato de um cone circular invertido, com base de raio e
altura igual a . Se a água está a sendo bombeada para o tanque a uma taxa de ,
encontre a taxa na qual o nível da água está a aumentando quando a água estiver com
de profundidade.
Ver solução completaQuestão 104
Uma partícula se move sobre a elipse ( e medidos em metros) deslocando-se no sentido anti-horário. No instante em que ela passa pelo ponto , sua coordenada decresce a uma taxa de . Quão rápido está variando a distância da partícula à origem nesse instante ?
Ver solução completaQuestão 105
Uma viga de de comprimento está apoiada em uma parede e o seu topo desliza para baixo a
uma velocidade constante de . Determine a taxa de variação do ângulo agudo formado pela
viga e pelo chão no instante em que o topo da viga se encontra a do chão.
Ver solução completaQuestão 106
Uma bola de ferro esférica com 8 cm. de diâmetro está coberta com uma camada de gelo de espessura uniforme. Se o gelo derrete com uma taxa de , a que taxa a espessura do gelo diminuirá quando tiver . de espessura? A que taxa a área da superfície externa do gelo diminuirá?
Ver solução completaQuestão 107
Calcule a taxa de variação do volume de um balão esférico em relação ao seu raio, quando o raio do balão for igual a
Ver solução completaQuestão 109
(4) A área de uma coroa circular com raios interno e externos variáveis se mantém constante e igual a . A área do círculo exterior varia a uma taxa de . Com qual velocidade varia o perímetro do círculo interior quando a sua área é ?
Ver solução completaQuestão 111
Considere um círculo inscrito em triângulo equilátero. Conforme o raio do círculo aumenta, o triângulo também aumenta, de forma que o primeiro esteja sempre inscrito no segundo. Sabendo que o raio do círculo varia a uma taxa de , qual a taxa de variação da área do triângulo quando o raio do círculo alcançar ?
Ver solução completaQuestão 113
Na figura abaixo, o segmento mede e é tangente à circunferência de raio no ponto . O ponto é determinado pela interseção da circunferência com o segmento . O ponto inicia um movimento de descida, pela vertical, em direção ao ponto a uma taxa constante de .
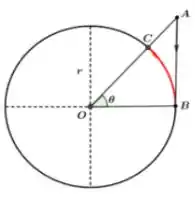
A taxa com que se movimenta o ponto , ao longo do arco , depois de segundos do ponto ter iniciado o seu movimento é
:
:
:
:
:
Ver solução completaQuestão 114
Um objeto com peso W é arrastado ao longo de um plano horizontal por uma força agindo ao
longo de uma corda atada ao objeto. Se a corda faz um ângulo com o plano, então a grandeza
da força é
onde µ é uma constante chamada coeficiente de atrito. Se W = 50 lb e = 0, 6, faça um esboço do gráfico de F como uma função de e use-o para localizar o valor de para o qual .
Ver solução completaQuestão 115
Um objeto com peso W é arrastado ao longo de um plano horizontal por uma força agindo ao
longo de uma corda atada ao objeto. Se a corda faz um ângulo com o plano, então a grandeza
da força é
onde µ é uma constante chamada coeficiente de atrito. Encontre a taxa de variação de F em relação a . Quando essa taxa de variação é igual a 0?
Ver solução completaQuestão 116
Um balão esférico está sendo enchido a uma taxa de .
a) Encontre a taxa de crescimento do raio do balão quando o diâmetro for igual a
b) Sabendo que num determinado instante o balão tem volume de , determine o volume após segundos
Ver solução completaQuestão 117
Um balão esférico está sendo enchido a uma taxa de . Encontre a taxa de crescimento do raio do balão quando o diâmetro for igual a . Volume da esfera é igual a , onde é o raio.
Ver solução completaQuestão 118
O número M de matrículas de um certo colégio vem crescendo a uma taxa de
estudantes por ano desde 2015. Se a matrícula em 2019 foi de 10.000 estudantes, responda:
(a) Qual teria sido a matrícula em 2015?
(b) Quantos estudantes são esperados em 2027 se o crescimento continuar na mesma taxa?
Ver solução completaQuestão 119
Considere que o valor monetário V (t) de uma coleção de antiguidades aumenta com a idade (tempo t).
- Escreva uma expressão para que signifique que a taxa de valorização da coleção em qualquer momento é 0.03 vezes seu valor naquele momento.
- Considerando constantes A e k não nulas, para que valores de k a seguinte função se encaixa no que você encontrou no item anterior? .
(c) Considerando adicionalmente que o valor da coleção era R$ 25.000 há 10 anos, escreva a função V (t) adequada e calcule em que ano se espera que o valor seja R$ 49.000. Use a
aproximação
Ver solução completaQuestão 120
Se um tanque contém, inicialmente, 5.000 galões de água, que escoa pelo fundo em 40 minutos,
então a Lei de Torricelli dá o volume V de água que restou no tanque depois de t minutos como
,em que
Encontre a taxa segundo a qual a água está escoando do tanque depois de: (a) 5 min, (b)
10 min, (c) 20 min e (d) 40 min.
Ver solução completaQuestão 121
Um objeto com peso W é arrastado ao longo de um plano horizontal por uma força agindo ao
longo de uma corda atada ao objeto. Se a corda faz um ângulo com o plano, então a grandeza
da força é
onde µ é uma constante chamada coeficiente de atrito. Encontre a taxa de variação de F em relação a .
Ver solução completaQuestão 122
Se um tanque contém, inicialmente, 5.000 galões de água, que escoa pelo fundo em 40 minutos,
então a Lei de Torricelli dá o volume V de água que restou no tanque depois de t minutos como
,em que
Em que instante o fluxo é mais rápido? E mais vagaroso? Resuma o que você encontrou.
Ver solução completaQuestão 123
8) A aresta de um cubo aumenta a uma taxa constante de . Determine a taxa de variação da área da superfície total do cubo no momento em que a medida da aresta é .
Questão 124
Considere que o valor monetário V (t) de uma coleção de antiguidades aumenta com a idade (tempo t).
- Escreva uma expressão para que signifique que a taxa de valorização da coleção em qualquer momento é 0.03 vezes seu valor naquele momento.
- Considerando constantes A e k não nulas, para que valores de k a seguinte função se encaixa no que você encontrou no item anterior? .
(c) Considerando adicionalmente que o valor da coleção era R$ 25.000 há 10 anos, escreva a função V (t) adequada e calcule em que ano se espera que o valor seja R$ 49.000. Use a
aproximação
Ver solução completaQuestão 125
Um reservatório possui a forma de um cone circular reto com o vértice para baixo, tem de profundidade e de diâmetro. Esse reservatório é esvaziado à razão constante de .
Determine a razão segundo a qual o nível de água está descendo no instante em que a superfície da água está a do topo.
Ver solução completaQuestão 126
Uma partícula percorre uma curva obedecendo à equação horária . Calcule a sua velocidade instantânea no instante
Ver solução completaQuestão 127
Em uma fazenda de psicultura, uma população de peixes é colocada dentro de um lago e colhido regularmente. Um modelo para variação da população é dada pela equação:
Em que é a taxa de nascimento dos peixes, é a população máxima que o pequeno lago pode manter (capacidade de suporte) e é a porcentagem da população que é colhida.
Qual o valor de correspondente à população estável?
Ver solução completaQuestão 128
4 - A área de um triângulo, com lados de comprimento e formando um ângulo á dada por.
a) Como se relaciona com , se e são constantes?
Ver solução completaQuestão 129
Considere que o valor monetário V (t) de uma coleção de antiguidades aumenta com a idade (tempo t).
- Escreva uma expressão para que signifique que a taxa de valorização da coleção em qualquer momento é 0.03 vezes seu valor naquele momento.
- Considerando constantes A e k não nulas, para que valores de k a seguinte função se encaixa no que você encontrou no item anterior? .
(c) Considerando adicionalmente que o valor da coleção era R$ 25.000 há 10 anos, escreva a função V (t) adequada e calcule em que ano se espera que o valor seja R$ 49.000. Use a
aproximação
Ver solução completaQuestão 130
Dê o domínio e esboce o gráfico, enfatizando as características vistas em sala, de cada função.
a)
Ver solução completaQuestão 131
Dê o domínio e esboce o gráfico, enfatizando as características vistas em sala, de cada função.
b)
Ver solução completaQuestão 132
Uma empresa comprou um equipamento em 1982 por R$1.200,00. Se o valor se deprecia de acordo com a fórmula
, onde é o valor e os anos passados após a compra, determine o valor do equipamento em 1986.
Ver solução completaQuestão 133
3 - Sejam e funções deriváveis de e seja a distância entre os pontos e no plano .
c) Como se relaciona com se é constante?
Ver solução completaQuestão 134
Uma partícula se move ao longo da parábola descrita pela equação . Determine os
pontos da curva nos quais as taxas de variação da abscissa e da ordenada são iguais.
Ver solução completaQuestão 135
Um reservatório cônico de de profundidade e de diâmetro está recebendo água na razão de . Determine:
a) A taxa de variação da altura do nível da água quando esta estiver a ;
Ver solução completaQuestão 136
5 - O comprimento de um retângulo está aumentando a uma taxa de e sua largura está aumentando a uma taxa de . Quando o comprimento for e a largura for quão rápido a área do retângulo está aumentando?
Ver solução completaQuestão 137
Um farol está a de uma praia reta e lança sobre ela um foco de luz. Se o foco gira com velocidade angular de , determine a velocidade com que a luz percorre a praia quando o foco estiver a do ponto da praia mais próximo do farol.
Ver solução completaQuestão 138
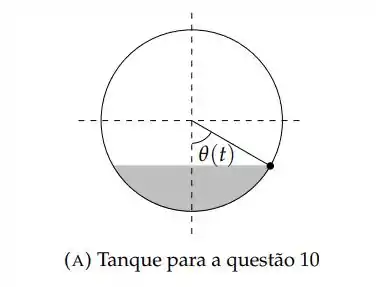
Uma mangueira está enchendo um tanque de gasolina que tem o formato de um cilindro “deitado” de diâmetro 2m e comprimento 3m. A figura 2a representa uma seção transversal do tanque no instante t. O ângulo θ varia de zero (tanque vazio) a π (tanque cheio). No instante em que a altura h do líquido é de 0.5m, a vazão é de 0.9m3/min. Determine a taxa de variação do ângulo θ nesse instante. Determine também a taxa de variação da altura h do neste mesmo instante.
Questão 139
2.8. Suponha que sobre um certo aberto o potencial elétrico é dado por .
a. Ache a taxa de variação do potencial em na direção do vetor .
Ver solução completaQuestão 140
2.8. Suponha que sobre um certo aberto o potencial elétrico é dado por .
b. Qual a direção e sentido em que a taxa do potencial elétrico, em , é a maior possível? E a menor possível?
Ver solução completaQuestão 141
Quando o último vagão de um trem passa por baixo de um viaduto, um carro cruza o viaduto numa rodovia perpendicular aos trilhos e a acima deles. O trem está a e o carro a . Com que velocidade se afastam um do outro após ?
Ver solução completaQuestão 142
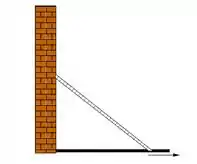
Uma escada com de comprimento está apoiada numa parede vertical. Se a base da escada for puxada horizontalmente, afastando-se da parede a , qual a velocidade com que a parte superior da escada estará deslizando ao longo da parede, quando a sua base estiver a da parede?
Questão 143
Um quadro de de altura é colocado em uma parede de tal forma que sua base esteja no mesmo nível dos olhos de um observador que está se aproximando da parede a uma velocidade de . Com que velocidade a medida do ângulo de visão do quadro estará variando quando o observador estiver a da parede?
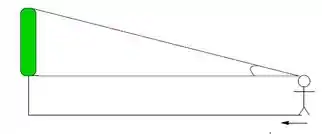
Questão 144
Um retângulo possui lados que variam com o tempo e está inscrito numa região triangular conforme a figura abaixo. Determine com que taxa a área do retângulo está variando no instante em que sua altura mede e está aumentando à taxa de . Nesse instante a área está aumentando ou diminuindo?
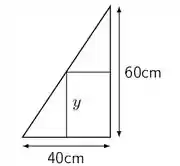
Questão 145
Um balão eleva-se verticalmente do solo à razão de . Quando o balão está a do solo, passa exatamente sob ele um automóvel viajando a velocidade de . Com que velocidade varia, (quatro) segundo após, a distância entre eles?
Ver solução completaQuestão 146
Um fusca viaja à razão de aproxima-se de um cruzamento. Quando o fusca está a do cruzamento um caminhão que viaja à razão de atravessa o cruzamento. O fusca e o caminhão estão em rodovias que formam um ângulo reto. Com que rapidez separam-se o fusca e o caminhão depois que o caminhão passou pelo cruzamento?
Ver solução completaQuestão 147
Uma caixa está sendo puxada por uma corda que passa por uma roldana presa a acima do solo. Determine a taxa de variação do ângulo , indicado na figura abaixo, no instante em que a caixa se encontra a do ponto , situado abaixo da roldada, sabendo que a caixa se desloca a .
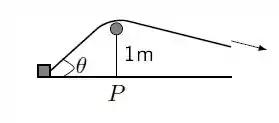
Questão 148
Um triângulo está inscrito num semicírculo de diâmetro conforme a figura abaixo. Sabendo que o vértice varia sobre o semicírculo e que o lado aumenta à razão de , determine a taxa com a qual a área do triângulo varia no instante em que o lado mede .
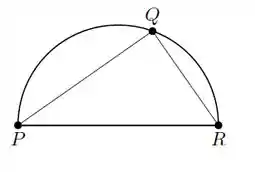
Questão 149
Dois lados paralelos de um retângulo aumentam à razão de , mas os outros dois lados diminuem de tal modo que a figura permaneça um retângulo de área constante igual a . Qual a velocidade com que o perímetro varia quando o lado que aumenta mede ?
Ver solução completaQuestão 150
Dois carros, um dirigindo-se para o leste à razão de e o outro para o sul à razão de , estão viajando em direção à interseção das duas rodovias. À que razão os carros aproximam-se um do outro, no instante em que o primeiro (direção leste) estiver a e o segundo (direção sul) a da interseção?
Ver solução completaQuestão 151
Uma calha horizontal possui de comprimento e tem como seção transversal um triângulo isósceles de de base e de altura conforme mostra a figura abaixo.
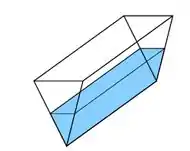
Devido à chuva, a água em seu interior está se elevando. Quão rápido o volume de água em seu interior estará aumentando no instante em que o nível da água for de e estiver aumentando a uma razão de .
Ver solução completaQuestão 152
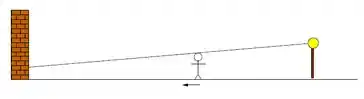
Uma mulher de de altura caminha em direção a um muro a uma razão de . Diretamente atrás dela e a do muro está um refletor acima do nível do solo.
Quão rápido o comprimento da sombra da mulher estará variando no muro quando ela estiver a meio caminho entre o refletor e o muro? A sombra está esticando-se ou encurtando-se?
Questão 153
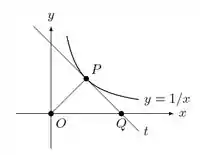
Na figura abaixo, é o ponto de tangência da reta com a curva . Sabendo que o ponto se desloca sobre a curva mostre que:
(b) A taxa de variaç��o da área do triângulo independe da velocidade com que o ponto se desloca.
Questão 154
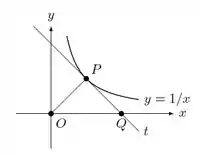
Na figura abaixo, é o ponto de tangência da reta com a curva . Sabendo que o ponto se desloca sobre a curva mostre que:
(a) O triângulo é sempre isósceles.
Questão 155
Considere a função no ponto encontre:
- A derivada direcional na direção de
- A taxa de variação máxima nesse ponto e a direção em que ela ocorre.
Questão 156
Considere a função no ponto encontre:
- A derivada direcional na direção de
- A taxa de variação máxima nesse ponto e a direção em que ela ocorre.
Questão 157
2.8. Suponha que sobre um certo aberto o potencial elétrico é dado por .
c. Qual o valor dessa taxa máxima?
Ver solução completaQuestão 158
Em cada item a seguir, encontre os intervalos de crescimento e decrescimento da função dada. Em seguida, determine seus pontos de máximo e mínimo locais (se existirem).
(b)
Ver solução completaQuestão 159
Em cada item a seguir, encontre os intervalos de crescimento e decrescimento da função dada. Em seguida, determine seus pontos de máximo e mínimo locais (se existirem).
(d)
Ver solução completaQuestão 160
Determine os extremos relativos, os intervalos de crescimento e decrescimento das seguintes funções:
Questão 161
Determine os extremos relativos, os intervalos de crescimento e decrescimento das seguintes funções:
Questão 163
Um círculo possui raio inicial de 1m e começa a crescer de tal forma que sua área aumenta a uma taxa de . Encontre a taxa de variação do raio do círculo quando seu raio mede 5 cm.
Ver solução completaQuestão 164
Um homem de 2 m de altura se move em direção a um a poste de luz a uma velocidade de 5 m/s. Do alto deste poste, uma lâmpada ilumina o homem e projeta uma sombra. Quando a distância entre o homem e o poste é de 4 m:
(a) Com que velocidade a ponta da sobra se move?
(b) Qual a taxa de varia ̧c ̃ao do comprimento da sombra?
Ver solução completaQuestão 165
Num filtro com formato de cone, como na figura 3a, um líquido escoa da parte superior para a parte inferior passando por um orifício de dimensões desprezíveis. Num certo instante, a altura H do líquido depositado na parte inferior é 8 cm, a altura h do líquido da parte superior é 10 cm e h está diminuindo a uma taxa de variação instantânea de 2 cm/min. Calcule a taxa de variação de H em relação ao tempo nesse instante.
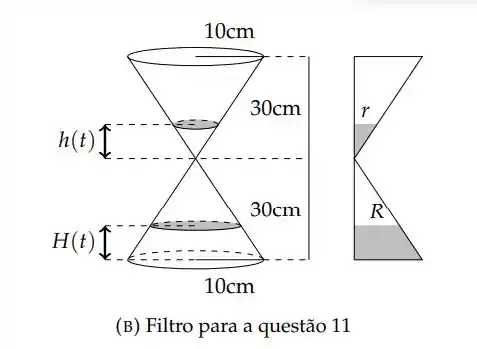
Questão 166
Uma quantidade bastante conhecida na Física é o momento, que é dado pelo produto da massa pela velocidade: . A força agindo sobre o objeto é a taxa de variação do momento em relação ao tempo: . Assumindo a massa do objeto como constante, temos , que é a Segunda Lei de Newton. No contexto de mecânica relativística, a massa do objeto não é constante e varia conforme sua velocidade: . Em que é a massa de partícula em repouso e é a velocidade da luz. Usando que e que a massa varia conforme a mecânica relativística, mostre que
Ver solução completaQuestão 167
2 - Suponha que o raio e a área de um círculo sejam funções deriváveis de . Escreva uma equação que relaciona a taxa de variação da área com a taxa de variação de .
Ver solução completaQuestão 168
6 - Cada lado de um quadrado está aumentando a uma taxa de . A que taxa a área do quadrado está aumentando quando a área do quadrado for ?
Ver solução completaQuestão 169
4 - A área de um triângulo, com lados de comprimento e formando um ângulo á dada por.
c) Como se relaciona com , e se nem , nem e nem são constantes?
Ver solução completaQuestão 170
3 - Sejam e funções deriváveis de e seja a distância entre os pontos e no plano .
a) Como se relaciona com se é constante?
Ver solução completaQuestão 171
3 - Sejam e funções deriváveis de e seja a distância entre os pontos e no plano .
b) Como se relaciona com e se nem nem são constantes?
Ver solução completaQuestão 172
4 - A área de um triângulo, com lados de comprimento e formando um ângulo á dada por.
b) Como se relaciona com e se apenas é constante?
Ver solução completaQuestão 173
7 - Um tanque cilíndrico com raio de está sendo cheio com água a uma taxa de . Quão rápido a altura da água está aumentando?
Ver solução completaQuestão 174
8 - O raio de uma esfera está aumentando a uma taxa de . Quão rápido o volume está aumentando quando o diâmetro for ?
Ver solução completaQuestão 175
9 - Dois carros iniciam o movimento partindo de um mesmo ponto. Um viaja para o sul a e o outro viaja para o oeste a . A qual taxa a distância entre os carros está aumentando duas horas depois?
Ver solução completaQuestão 176
16 - Está vazando água de um tanque em forma de um cone invertido a uma taxa de . Ao mesmo tempo, a água está sendo bombeada para dentro do tanque a uma taxa constante. O tanque tem de altura e diâmetro no topo de . Se o nível da água estiver subindo a uma taxa de quando a altura da água for , encontre a taxa segundo a qual a água está sendo bombeada para dentro do tanque.
Ver solução completaQuestão 177
15 - Um homem começa a andar para o norte a a partir de um ponto . Cinco minutos depois uma mulher começa a andar para o sul a de um ponto ao leste de . A que taxa as pessoas estão se distanciando após a mulher começar a andar?
Ver solução completaQuestão 178
Em cada item a seguir, encontre os intervalos de crescimento e decrescimento da função dada. Em seguida, determine seus pontos de máximo e mínimo locais (se existirem).
(a)
Ver solução completaQuestão 179
O governo estima que o custo, em milhares de reais, para despoluir de uma reserva de água doce é dado pela função
- Calcule, usando a regra do quociente, a taxa de variação do custo com respeito ao percentual de despoluição, quando a reserva está despoluída.
Questão 180
3. (b) Suponha que agora se sabe que o objeto circular que está sendo observado é na verdade a seção transversal de um objeto esférico. Encontre a taxa de variação do volume quando o raio é .
Ver solução completaQuestão 181
3. (c) Suponha agora que a taxa de variação da área da seção transversal circular é quando o raio é . Encontre a taxa de variação do volume quando o raio é .
Ver solução completaQuestão 182
O número M de matrículas de um certo colégio vem crescendo a uma taxa de
estudantes por ano desde 2015. Se a matrícula em 2019 foi de 10.000 estudantes, responda:
(b) Quantos estudantes são esperados em 2027 se o crescimento continuar na mesma taxa?
Ver solução completaQuestão 183
Um peso está preso a uma das extremidades de uma corda de de comprimento que passa por uma polia situada a acima do solo. A outra extremidade da corda, que se encontra esticada, está presa a um caminhão por um ponto situado acima do solo. Sabendo que o caminhão se afasta horizontalmente a uma velocidade de , determine a taxa de variação da altura do peso no instante em que o mesmo estiver a acima do solo.
Ver solução completaQuestão 184
Uma partícula se movimenta ao longo de uma reta real seguindo a função horária dada por , com derivável e unidades no sistema MKS. Supondo , calcule a velocidade da partícula no instante .
Ver solução completaQuestão 185
Um tanque cilíndrico com raio está sendo enchido com água a uma taxa de . Qual é a taxa de crescimento da altura da água no tanque?
Ver solução completaQuestão 186
A Lei de Gravitação de Newton diz que a intensidade da força exercida por um corpo e massa sobre um corpo de massa é
Em que é a constante gravitacional e é a distância entre os corpos. Calcule e explique seu significado. O que o sinal de menos indica?
Ver solução completa