Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.2 - Ex. 19

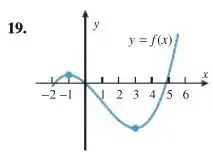
19-20. Esboce o gráfico de e de da função cujo gráfico é dado.

Passo 1

Então galera, para plotarmos o gráfico de temos que observar o gráfico que nos foi dado nas proximidades dos máximos e mínimos, a fim de deduzir qual o sinal da derivada nesses intervalos. A função tem pontos críticos em e em , certo? Então vamos analisar o gráfico de nas proximidades desses pontos!

Para a derivada é decrescente;

Para a função tem um mínimo;

Para a derivada é crescente.

Tendo em vista esses resultados, temos que o gráfico de será uma parábola, do tipo:

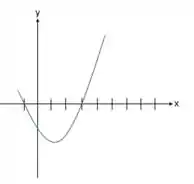
Passo 2

Agora quanto a derivada segunda, temos que analisar as concavidades, pessoal!

Para a função tem concavidade para baixo;

Para a função tem um ponto de inflexão;

Para a função tem concavidade para cima.

Tendo em vista esses resultados, temos que o gráfico de será mais ou menos assim:

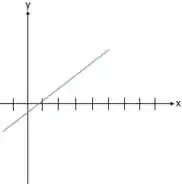
E esses são os esboços de e de , galera!

Resposta

Esboço de :

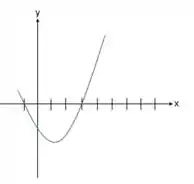
Esboço de :

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontrar os pontos de máximo e mínimo relativos das seguintes funções, se existirem. Fazer um esboço do gráfico e comparar os resultados.c) h x = 1 3 x 3 + 3 x 2 - 7 x + 9

Encontrar os intervalos de crescimento, decrescimento, os máximos e os mínimos relativos das seguintes funções:m) g x = 10 - x - 3 2 , x ≤ - 2 5 x - 1 ,- 2x ≤ - 1 - 91 + x - 2 2 , x- 1

Encontrar os pontos de máximo e mínimo relativos das seguintes funções, se existirem. Fazer um esboço do gráfico e comparar os resultados.d) h x = 1 4 x 4 - 5 3 x 3 + 4 x 2 - 4 x + 8

Encontrar os pontos de máximo e mínimo relativos das seguintes funções, se existirem. Fazer um esboço do gráfico e comparar os resultados.e) f t = t 2 , t0 3 t 2 , t ≥ 0

Encontrar os intervalos de crescimento, decrescimento, os máximos e os mínimos relativos das seguintes funções:l) f x = 1 + x , x- 1 1 - x 2 , x ≥ - 1