Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.10 - Ex. 9c

Encontrar os pontos de máximo e mínimo relativos das seguintes funções, se existirem. Fazer um esboço do gráfico e comparar os resultados.

c)

Passo 1

Então pessoal, para descobrirmos quais são os máximos e mínimos de uma função existe um método bastante eficaz que utiliza derivação, assim como abordado no capítulo 5 da Flemming e Gonçalves. Vocês devem concordar que se um ponto é ponto de máximo ou mínimo, então sua derivada é nula nesse mesmo ponto, não é? Sendo assim, derivando nossa função para obter os pontos críticos, obteremos:

Igualando a zero:

Então e são os pontos críticos da nossa função.

Passo 2

Uma vez descoberto os pontos críticos da nossa função, devemos utilizar o teste da derivada segunda para saber se os pontos são de máximos ou de mínimos, tudo bem? Se a derivada segunda no ponto crítico for MAIOR do que zero, então se trata de um ponto de mínimo. Caso contrário, se a derivada segunda no ponto crítico for MENOR do que zero, então se trata de um ponto de máximo. Sendo assim, se derivarmos nossa função pela segunda vez, teremos:

Portanto, podemos concluir que é um ponto de mínimo e é um ponto de máximo! Resumindo, temos que:

Pontos de máximo: ;

Pontos de mínimo: .

Passo 3

Se esboçarmos o gráfico da função, teremos:

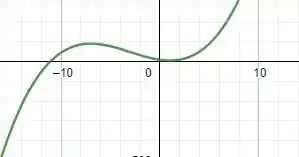
Observando o gráfico podemos concluir que nosso resultado é bem satisfatório! Assim como calculamos, é um ponto de máximo e é, de fato, um ponto de mínimo!