Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.18 - Ex. 19
19.Um tanque cilíndrico reto de raio de e altura está cheio de água. Achar o trabalho efetuado para esvaziar o tanque, pela parte superior.
Passo 1
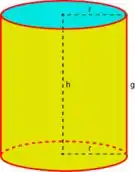
Para essa questão, teremos que pegar um elemento infinitesimal, ou seja, muito pequeninho e levar do fundo até a borda do tanque. O tanque sendo um cilindro reto, esse elemento infinitesimal não terá mudança no tamanho do raio na subida!
Vem comigo!!
Passo 2
Antes de fazermos quaisquer contas, iremos determinar os pontos de referência e como nossa intuição sugere, vamos fazer com que o ponto zero seja no fundo do poço e o ponto seja na borda do tanque.
Agora precisamos determinar a área desse elementinho de volume pequeno.
Ora, o raio dele não muda durante a subida, então a sua área é:
Conforme a água vai escapando pela borda o peso da água vai diminuindo, então quando o embolo deslocar metros, sobrará de água .
Então o volume após o deslocamento de metros é:
E multiplicando pela peso da água por que é , temos que a força é:
Passo 3
Integrando a força variável de até . Temos:
Nota: O gabarito dá apenas a resposta , acredito que eles tenham esquecido do , pois todas as outras respostas vem com .