Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 5.10 - Ex. 1g
1-Encontrar, se existirem, os pontos de máximo e de mínimo globais das funções:
g)
Passo 1
Galera, eu já adianto que a melhor forma de resolver esse item é através do gráfico dessa função.
A primeira coisa que temos que saber é que tipo de superfície nós temos.
Bom, vamos começar completando quadrados .
Passo 2
Galera, se nós olhássemos só para o que está dentro da raiz perceberíamos que temos uma esfera. No entanto, a raiz nos diz que o z só admite valores positivos, portanto o gráfico da função coincide com a superfície de uma meia esfera.
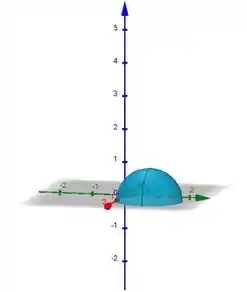
Passo 3
Analisando o gráfico percebemos que no ponto (1,1) a função alcança o seu máximo global, quando o z é igual a 1. Já os pontos de mínimo global são aqueles sobre a circunferência de centro (1,1) e raio 1.
Resposta
O ponto de máximo global é (1,1). Já os pontos de mínimo global são aqueles que estão sobre a circunferência de centro (1,1) e raio 1.