20- A altura de ondas em mar aberto depende da rapidez do vento e do tempo durante o qual o vento se manteve naquela intensidade. Os valores da função são apresentados na seguinte tabela.
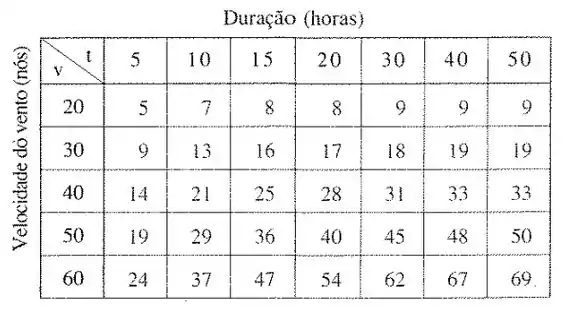
Use a tabela para determinar uma aproximação linear da função altura da onda quando está próximo de . Em seguida, estime a altura das ondas quando está ventando por a .
Passo 1
Oie, tudo bem? Vamos resolver essa atividade aqui.
A gente tem a tabela abaixo:
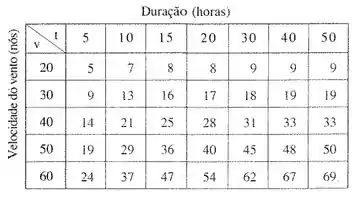
Aqui a gente tem as informações sobre a velocidade do veto em determinado tempo .
A gente precisa com ajuda dessa tabela, estimar a altura das ondas em . Para isso iremos utilizar a linearização.
A formula de linearização para o nosso caso é dada por:
em que é o ponto em que queremos linearizar, enquanto e são as derivadas parciais em relação a velocidade e o tempo.
Passo 2
Para estimar o valor de vamos ter que utilizar o ponto da tabela que está mais próximo do que queremos que seria e para isso temos o ponto mais próximo em . A função de linearização para será igual a:
Onde e:
Fica o dever de calcular as derivadas em e em nesses pontos e para isso vamos pegar a média da variação do ponto de interesse com o ponto anterior e com o ponto seguinte de modo que teremos:
Para esse caso iremos utilizar , pois temos os dados das velocidades aqui em em :
Entendeu? Usa a definição de derivada por limite nos pontos anterior e posterior (na direção de , que é a vertical na tabela) e depois fazer a média disso, isso nos dá a derivada na direção no ponto que queremos na tabela.
Fazendo a conta temos:
Agora para calcular :
Aqui temos que analisar a variação em (horizontal na tabela) do ponto anterior e posterior e notar que varia pro anterior (sinal negativo) e pro próximo.
Dessa forma:
Passo 3
Dessa forma a equação de linearização fica:
Agora substituindo os valores de e nessa equação de linearização nós teremos:
Utilizei (unidade de altura) pois ele não fala se essa altura é em pés, metros, quantos carros populares de altura hahaha então é um genérico.