Utilize coordenadas polares para determinar o volume do sólido dado.

Limitada pelo paraboloide e pelo plano .

O sólido que estamos trabalhando é limitado por um paraboloide e um plano.

Um paraboloide é nada mais que uma parábola rotacionada em torno de um eixo. Nesse caso:

Rotacionada em torno de .

Desenhando junto com o plano fica assim:

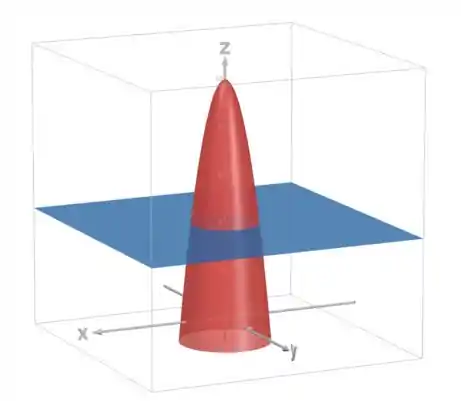
O volume que nós queremos é desse sólido acima do plano e abaixo do paraboloide, então:

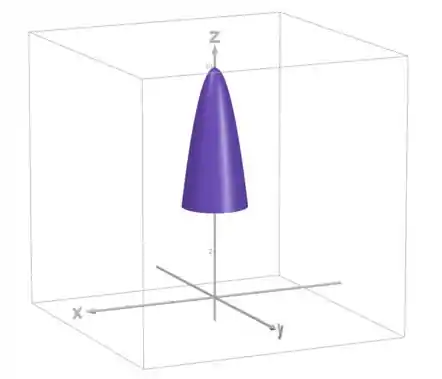
Então já definimos quem é e . Já que precisamos que no domínio que estamos trabalhando, então:

Agora vamos definir o domínio desse sólido. Ele vai ser a sua projeção sobre o plano .

Percebe que o sólido vai afunilando desde a sua base (que é a interseção das duas superfícies). Vamos ver qual a equação dessa base:

Então

Dividindo tudo por :

Ou seja, a base do sólido é um círculo de raio . Como acima dele o sólido só afunila, essa vai ser também a sua projeção no plano e, portanto, o domínio :

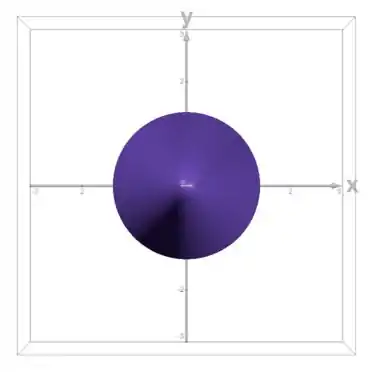
De fato, é uma região circular, como a gente previu. Vamos usar coordenadas polares:

Como é um círculo inteiro de raio :

A integral fica assim:

Vamos colocar em evidência pra fora da integral:

Como estamos em coordenadas polares:

Já que .

Então:

Agora só falta calcular essa integral! Fazemos de dentro pra fora. Primeiro em função de com constante:

Resolvendo a integral:

Como

Por último, tiramos o da integral e calculamos:

Então