Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.4 - Ex. 4
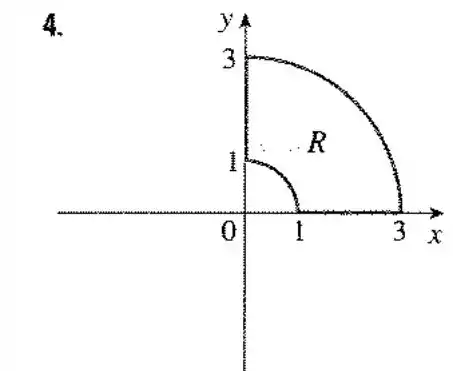
Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva como uma integral iterada, onde é uma arbitrária qualquer contínua em .
Passo 1
Fala, galera!
A questão que a gente precisa resolver é bem simples. Ela nos deu um gráfico e pede pra gente representar, ou em coordenadas polares ou cilíndricas, como uma integral iterada dessa forma:
Moleza, né, galera?
Passo 2
Nesse nosso caso é melhor utilizar coordenadas polares por termos duas funções circulares, e escolhendo desta forma, os círculos têm variando de 0 até e para compor essa área vai de até .
Logo, os limites de integração serão:
Relembrando que em coordenadas polares, temos
Dessa forma, a integral em coordenadas polares ficará assim:
Show de bolinha! 😊
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 9-22, substitua a integral cartesiana por uma integral equivalente. Em seguida, calcule a integral polar. ∫ 0 2 ∫ 0 4 - y 2 x 2 + y 2 d xd y
Nos Exercícios 9-22, substitua a integral cartesiana por uma integral equivalente. Em seguida, calcule a integral polar. ∫ - 1 1 ∫ 0 1 - x 2 d yd x
Nos Exercícios 1-8, descreva a região dada em coordenadas polares.
Nos Exercícios 1-8, descreva a região dada em coordenadas polares.A região delimitada pela circunferência x 2 + y 2 = 2 x
Nos Exercícios 9-22, substitua a integral cartesiana por uma integral equivalente. Em seguida, calcule a integral polar. ∫ - a a ∫ - a 2 - x 2 a 2 - x 2 d yd x