Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.2 - Ex. 23
21-24 Use o gráfico de mostrado em cada figura para estimar todos os valores de nos quais tem (a) mínimos relativos, (b) máximos relativos e (c) pontos de inflexão; (d) esboce um gráfico rudimentar de uma função com a derivada dada.
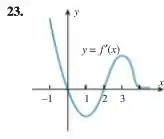
Passo 1
Galerinhaaa, para resolver essa questão nós temos que analisar esse gráfico.
Como e nós podemos dizer que e são pontos críticos, agora, nos resta saber se eles são pontos de máximo ou mínimo, né ?
Bom... Se nós tivéssemos uma expressão para , o que nós faríamos ???
Pelo teste da primeira derivada deveríamos, primeiro, achar os pontos críticos, ou seja, igualar a função a zero, ahhhh, mas isso nós já temos...
Depois nós teríamos que checar como a se comporta antes e depois de .Como o exercício nos deu o gráfico fica fácil analisar essa função.
Para , à sua esquerda e à sua direita. Isso quer dizer que esse é um máximo relativo.
Para à sua esquerda e à sua direita. Isso quer dizer que esse é um mínimo relativo.
Passo 2
Agora, temos que ver se temos algum ponto de inflexão.
Gente, olha só, quando nós fazemos o teste da segunda derivada para encontramos os pontos de inflexão, nós igualamos à zero e, fazemos um estudo de sinal da função em torno dos pontos em que . Dessa forma,
Quando vai de , deixa de ser crescente e passa a ser decrescente, ou seja, nós temos um ponto de inflexão.
Quando vai de , deixa de ser decrescente e passa a ser crescente, ou seja, nós temos um ponto de inflexão. Ok ?
Analisando o gráfico, nós percebemos que em , a função que era decrescente passa a ser crescente e ocorre exatamente o contrário. Isso quer dizer que, para e , temos 2 pontos de inflexão.
Resposta
a)
b)
c)