Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.1 - Ex. 72

Em 7 de maio de 1992, o ônibus espacial Endeavour foi lançado na missão STS-49, cujo objetivo era instalar um novo motor de arranque no satélite de comunicação Intelsat. A tabela dá os dados de velocidade para o ônibus espacial entre a partida e a ejeção dos foguetes auxiliares.

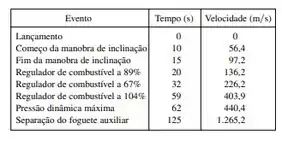
  1. Use uma calculadora gráfica ou computador para encontrar o polinômio cúbico que melhor modele a velocidade do ônibus para o intervalo de tempo. Faça então o gráfico desse polinômio.
  2. Encontre um modelo para a aceleração do ônibus e use-o para estimar os valores máximo e mínimo da aceleração durante os primeiros 125 segundos.

Passo 1

Nessa questão temos uma tabela de valores para o tempo e velocidade e inicialmente temos que encontrar um polinômio cúbico que modele essa velocidade.

Para inicio de resolução precisamos plotar o gráfico no Excel, por exemplo, para encontramos a equação v ( t ) . Okay? Okay!!

Assim, temos

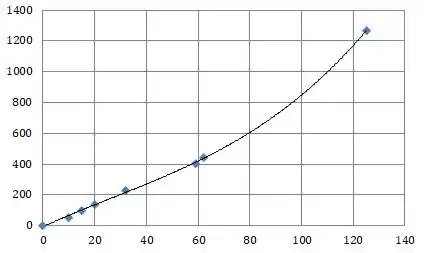
Usando a aproximação cúbica do excel, encontramos o seguinte polinômio cúbico.

v t = 0,0004 t 3 - 0,0352 t 2 + 7,6143 t - 6,4899

Assim, já matamos a letra a). Agora para a letra b), temos que estimaros valores máximos e mínimos da aceleração.

Para isso vamos inicialmente derivar a velocidade para encontrar a aceleração, afinal:

a t = d v t d t

Ou seja, a aceleração é a derivada da velocidade.

Depois para encontrar onde a aceleração é máxima e mínima dentro os 125 segundos, vamos derivar essa expressão da aceleração e igualar a zero.

a ' t = 0

E os valores de t onde a derivada é zero serão candidatos de máximo e mínimo.

Depois vamos substituir esses valores na aceleração para encontrar qual a aceleração nesses tempos.

Por fim, vamos substituir o tempo inicial do intervalo e o final, pois pode ser que a aceleração máxima ou mínima esteja nas extremidades do intervalo.

Feito tudo isso, vamos comparar os valores para encontrar qual o máximo e qual o mínimo.

Passo 2

Para encontrarmos um modelo para a aceleração, derivamos v ( t ) , logo

a t = 0,0012 t 2 - 0,0704 t + 7,6143

Encontrar os valores de máximo e mínimo é só derivar novamente e igualar a zero:

a ' t = 0,0024 t - 0,0704

Como queremos que a ' t = 0 , ficamos com:

0 = 0,0024 t - 0,0704

t = 29,33

Para saber durante os primeiros 125 segundos, vamos aplicar o tempo que encontramos derivando e igualando a zero e também os tempos extremos do intervalo de 125 s .

a 0 = 0,0012 0 2 - 0,0704 0 + 7,6143

a 0 = 7,6143   m / s 2  

E

a 29,33 = 0,0012 29,33 2 - 0,0704 29,33 + 7,6143

a 29,33 = 6,58177   m / s 2

E

a 125 = 0,0012 125 2 - 0,0704 125 + 7,6143

a 125 = 17,5643   m / s 2

Logo, a aceleração máxima está em t = 125 s e a 125 = 17,5643   m / s 2 e a aceleração mínima em t = 29,33 s e a 29,33 = 6,58177   m / s 2 .

Resposta

  1. Gráfico.
  2. a aceleração máxima está em t = 125 s e a 125 = 17,5643   m / s 2 e a aceleração mínima em t = 29,33 s e a 29,33 = 6,58177   m / s 2 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O gráfico da derivada f ' de uma função f está mostrado. (a) Em quais intervalos f é crescente ou decrescente? (b) Em que valores de x a função f tem um mínimo ou máximo local?
f x = x 3 - 12 x + 1 Encontre os intervalos nos quais f é crescente ou decrescente. Encontre os valores máximo e mínimo locais def . Encontre os intervalos de concavidade e os pontos de inflexão.
Esboce o gráfico de uma função que tenha dois máximos locais e um mínimo local, mas nenhum mínimo absoluto.Esboce o gráfico de uma função que tenha três mínimos locais, dois máximos locais e sete núme
Encontre os números críticos da funçãof (x) = x^3 + x^2 - x
Encontre os números críticos da funçãof (x) = 5 x^2 + 4 x