Para cada um dos números , estabeleça se a função cujo gráfico é dado tem um máximo ou mínimo absoluto, um máximo ou mínimo local, ou nem máximo nem mínimo.
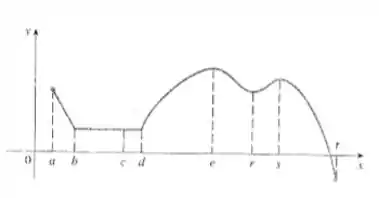
Passo 1
Fala aí, tudo belezinha com você?
Essa questão dá pra gente o seguinte gráfico
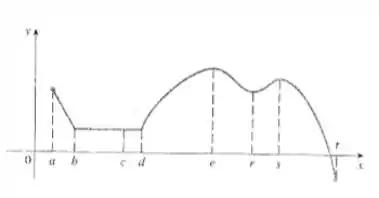
E pede pra gente, para cada um dos números , estabelecer se a função tem um máximo ou mínimo absoluto, um máximo ou mínimo local, ou nem máximo nem mínimo.
Antes de ir direto para essa resolução vamos lembrar que:
O mínimo absoluto é o menor valor da função dentro do intervalo e o máximo absoluto é o maior valor.
Já máximos ou mínimos locais ocorrem quando a função tem um “pico” ou “vales”.
Devemos lembrar que um número pode ser um máximo/mínimo local e não ser absoluto, e também pode ser máximo/mínimo absoluto mas não ser local (quando está nos extremos do intervalo).
Passo 2
Para cada número, vamos definir então qual o tipo de ponto é.
Número :
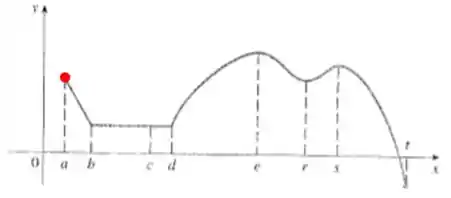
Não é um máximo local pois não há como comparar o lado esquerdo do ponto, já que ele está no limite do intervalo. Então não é máximo nem mínimo.
Passo 3
Número :
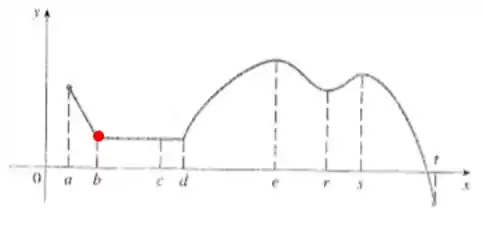
Os valores da função na esquerda próxima de são maiores que , e no lado direito são iguais. Podemos dizer então que temos aí um mínimo local.
Passo 4
Número :
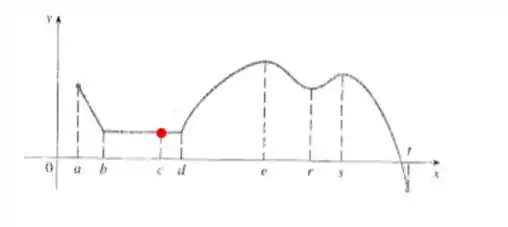
Se pegarmos um intervalo contendo que passe do número pela esquerda e passe do número pela direita, vemos que todos os valores da função no intervalo são menores que , então temos um mínimo local. Note que temos mínimos locais em todo o intervalo .
Passo 5
Número :
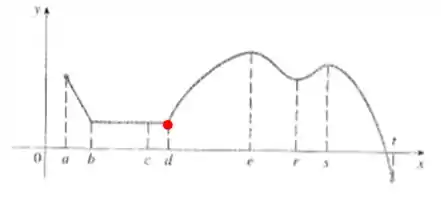
Pelos mesmos motivos dos pontos e , temos um mínimo local.
Passo 6
Número :
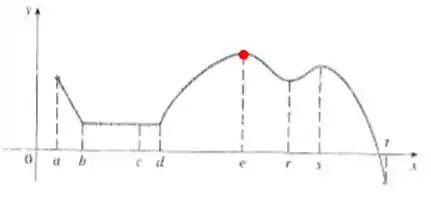
Os valores da função na esquerda e na direita próximos de são menores que , então temos um máximo local. Além disso, temos o ponto mais alto da função, então temos também o máximo absoluto.
Passo 7
Número :
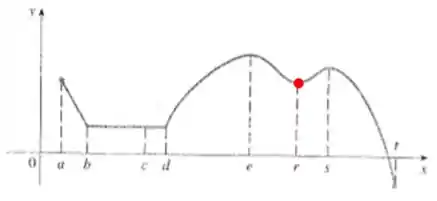
Os valores da função na esquerda e na direita próximos de são maiores que , então temos um mínimo local.
Passo 8
Número :
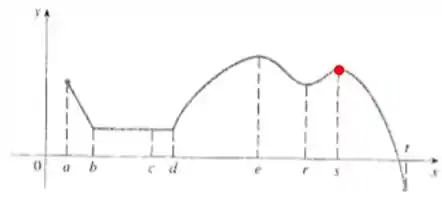
Os valores da função na esquerda e na direita próximos de são menores que , então temos um máximo local.
Passo 9
Número :
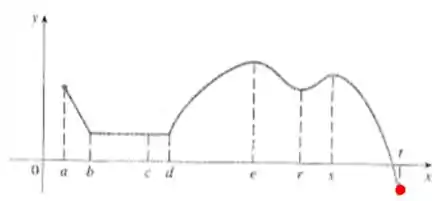
Não é um mínimo local pois está no extremo do intervalo. Mas é o menor valor da função, então é o mínimo absoluto.
Resposta
a: Nem máximo nem mínimo
b: Mínimo local
c: Mínimo local
d: Mínimo local
e: Máximo local e absoluto
r: Mínimo local
s: Máximo local
t: Mínimo absoluto