Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.Revisão - Ex. 22

22. A figura a seguir mostra um modelo para a variação das marés em um ponto interno da baía de San Francisco durantes um período de 24 horas. Encontre uma equação da forma y = y 0 + y 1 sin ⁡ ( a t + b ) para o modelo, supondo que t = 0 corresponda á meia noite.

Passo 1

Show de bolinhas meus dengo, o gráfico que ele deu pra gente é:

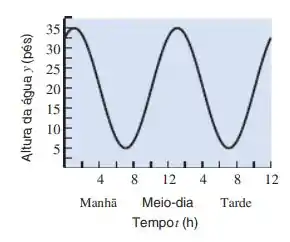
E partir dele, devemos encontrar os valores para a função y = y 0 + y 1 sin ⁡ ( a t + b ) .

Passo 2

Belezera, pra isso a gente pode lembrar o que cada termo significa, o y 1 é coeficiente do seno, ele que indicia o quão grande o valor de seno vai ficar, temos que a função vai de 5 até 35, logo o “tamanho” dela é de 30 unidades, e como:

- 1 ≤ sin ⁡ x ≤ 1

- 15 < sin ⁡ x ≤ 15

Traz isso pra gente, então temos y 1 = 15 .

Passo 3

O valor de y 0 representa o deslocamento da função f ( x ) ao longo do eixo y , nossa função seno está 20 unidades acima no eixo y , portanto y 0 = 20 . Para o valor de a , devemos lembrar que ele indica o quão esticada no eixo x , minha função está, lembrando que um período da função seno é 2 π e nesse caso temos exatamente 24 hrs, o que faz com que a = 1 .

Passo 4

O por fim para encontrarmos b , podemos pegar o ponto onde t = 0 , que vamos obter:

y = y 0 + y 1 sin ⁡ ( a t + b )

y = 20 + 15 sin ⁡ ( t + b )

y 0 = 20 + 15 sin ⁡ b

Logo, b = 14 π 45 , portanto, nossa função pde ser escrita como:

y = 20 + 15 sin ⁡ t + 14 π 45

Resposta

y = 20 + 15 sin ⁡ t + 14 π 45

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação c o s t = 1 está satisfeita.
Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função c o t g 7 4 π .
Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função t g 11 3 π .
Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função t g 7 4 π .
Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função c o t g 4 3 π .