Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.Revisão - Ex. 23
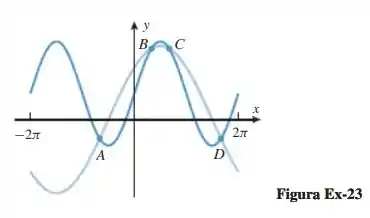
23. A figura em anexo mostra os gráfico das equações e para . Sem utilizar um recurso computacional, identifique cada uma das duas curvas pela sua equação e encontre as coordenadas dos pontos e indicados. Explique seu raciocínio.
Passo 1
Belezoca galera, o gráfico que ele deu pra gente foi
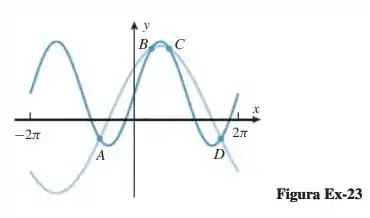
E as funções são e .
Passo 2
Para , temos que a primeira equação vale;
Portanto, só temos um função que é positiva em de acordo com o gráfico, e ela é , a curva de um azul mais escuro.
Passo 3
Agora, os pontos , são os pontos de interseção entre as curvas:
Resolvendo essa equação, chegamos que a solução geral é:
E como nosso intervalo é , temos os pontos:
Resposta
Exercícios de Livros Relacionados
Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação s e n t = - 1 está satisfeita.
Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação c o s e c t = 1 está satisfeita.
Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função c o t g - 9 2 π .
Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação s e n t = 0 está satisfeita.
Encontre todos os valores de t no intervalo [ 0,2 π ) em que a equação s e n t = 1 2 está satisfeita.