Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.Revisão - Ex. 40
40. a) Mostre que, para e , as equações
Têm as mesmas soluções.
b) Use o gráfico de para determinar os valores de com os quais a equação tem duas soluções positivas distintas.
c) Aproxime as soluções positivas de .
Passo 1
Belezuras galera, a letra (a), queremos mostra que para e , as equações:
Têm as mesmas soluções. Pra isso, a gente pode pegar alguma dessas equações e ver se conseguimos, a partir de alguma operaçõeszinhas, chegar na outra. Saca só, na primeira, podemos fazer o seguinte:
Bora aplicar o logaritmo natural dos dois lados:
Logo:
E como , temos que:
Passando o para um lado e para o outro temos:
O que é exatamente igual a outra equação.
Portanto, elas possuem as mesmas soluções.
Passo 2
Agora na letra (b), queremos saber os valores de com os quais a equação tem solução. Cruzando os gráfico de e temos:
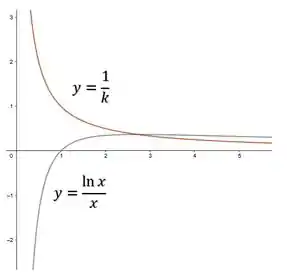
Elese se intersectam em , logo em temos a solução positiva :
Passo 3
Agora por fim, na letra(c), vamos aproximar as soluções positivas de . A partir da nossa relação temos que:
Temos agora que , logo:
E jogando essa equação na calculadora gráfica, obtemos:
Podemos aproximar nosso valores para e .
Resposta
- .
- .
- e .