Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.8 - Ex. 26
24. Use o método de Newton para encontrar todas as raízes da equação com precisão de oito casas decimais. Comece fazendo um gráfico para encontrar a aproximação inicial.
Passo 1
Aqui temos que encontrar a solução correta, com casas decimais, e como o próprio enunciado já diz, vamos desenhar os gráficos, e depois aplicar o método de Newton, preparados?
O Método de Newton é como um jogo de adivinhação inteligente para encontrar o ponto onde uma curva cruza o eixo x, ou outra curva.
Etapas:
Escolha Inicial: Vamos começar com um palpite inicial para o encontro das duas equações.
Iteração: Em cada passo, a gente usa a fórmula para obter uma nova aproximação , onde é a função e é sua derivada.
Convergência: O processo é repetido até que a diferença entre as aproximações sucessivas seja menor que um valor de tolerância pré definido (o critério de parada).
Critérios de Parada: para esse problema, temos a precisão de oito casas decimais!
É como tentar acertar o alvo no escuro, mas a cada tentativa você acende uma luzinha que te deixa mais perto de acertar em cheio!
Também podemos usar o método para encontrar quando duas funções se cruzam, para isso igualamos as duas, e passamos tudo para um único lado igualando a zero, assim podemos aplicar o método e encontrar o valor de nos pontos que há esse cruzamento.
Este método é eficaz quando a função é bem comportada e o palpite inicial está relativamente próximo da raiz verdadeira. Agora esse passo-a-passo que faremos para a nossa equação:
É nela que iremos aplicar o método, preparados?
Passo 2
Antes de começar vamos esboçar um gráfico.
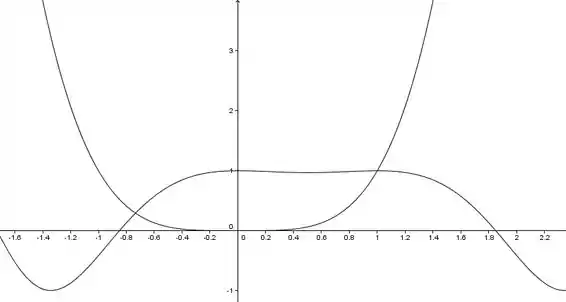
Aqui é só um esboço para ajudar a gente no chute inicial, portanto não precisa ser perfeito, pensa que é como uma função quadrática, mas com a base maior. Já a função , é uma função cosseno com a frequência maior, exceto entre o intervalo , onde a frequência será maior.
Mas porque ter ideia de como é gráfico é importante? Porque assim sabemos que serão raízes, e assim poderemos chutar melhor no começo e nos poupar trabalho.
Agora vamos transformar nossa equação em uma função, jogando tudo para o mesmo lado, essa será a nossa
Passo 3
Agora temos que derivar nossa
Aqui usaremos a regra da cadeia e a regra da potência:
Para a potência:
Para o cosseno, vamos de regra da cadeia, a derivada do de fora multiplicado pela derivada do de dentro:
Juntando tudo temos:
Agora aplicando na fórmula do método de Newton, temos:
Olhando o gráfico, podemos ver que é interessante pegar os pontos, pois eles são mais próximos do cruzamento das funções:
;
Passo 4
E agora vamos mostrar para a calculadora o porque ela veio ao mundo:
Para o ponto :
Fazendo as contas:
Opa, como deu igual já podemos parar, (que sorte!). Pois nos aproximamos o suficiente da raiz. Logo, a raiz aproximada de oito casas decimais será .
Para a próxima raiz, escolhemos , substituindo na fórmula:
Para :
Para :
Para , substituindo na fórmula:
Para :
Como , chegamos na repetição, então nossa raiz será .
Resposta
As raízes aproximadas de oito casas decimais são e