Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.9 - Ex. 17
17. Encontre a primitiva mais geral de cada uma das seguintes funções. (Verifique sua resposta derivando.)
Passo 1
E ai, blz?
A função dada é a seguinte:
E temos que encontrar a primitiva/integral dela, que nada mais é a função original que quando derivada nos dará essa função . E para comprovar que chegamos a função certa, vamos derivar voltar para a mesma do começo. Integral e derivada são operações opostas como multiplicar e dividir.
Para nos ajudar vamos fazer uso dessa tabela:
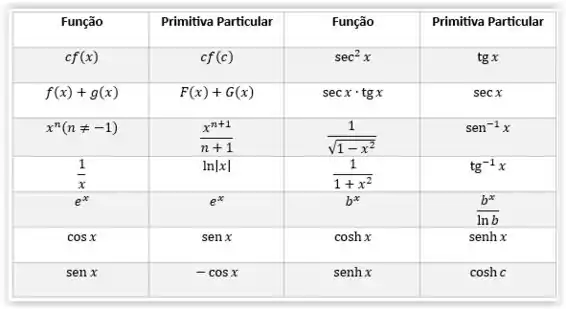
Preparados? Bora lá!
Passo 2
Para achar a primitiva/integral, vamos fazer o cada termo segundo a tabelinha:
E
Juntando tudo em :
Ajeitando tudo:
Passo 3
Agora vamos derivar para ver se está certo! Podemos usar a mesma tabela, mas agora olhando inversamente, temos a primitiva e queremos a função original:
E a derivada da constante é zero.
Organizando tudo:
Chegamos então que:
E com isso nossa primitiva está correta.