Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.2 - Ex. 25
25-32 Use a derivada dada para encontrar todos os pontos críticos de e, em cada um deles, determine se ocorre um máximo relativo, um mínimo relativo ou nenhum desses. Suponha, em cada caso, que seja contínua em toda parte.
25-
Passo 1
Gente, a primeira coisa que temos que lembrar aqui são as características de um ponto crítico. Para , por exemplo, ser um ponto crítico, ou ou não é diferenciável em .
Como o exercício já nos deu a primeira derivada, só precisamos igualar ela a zero. Então vamos lá!
Passo 2
Ou
Passo 3
Galera, agora, nós temos que ver o comportamento de nos seguintes intervalos:
- , , .
Nós podemos ver isso testando alguns valores na função.
Para :
Para :
Para :
Dessa forma,
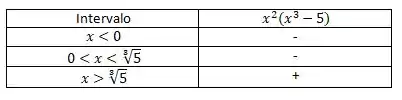
Mas afinal o que isso quer dizer ???
Como tem o mesmo sinal à direita e à esquerda de , não tem um extremo relativo no zero.
Como à esquerda de e à direita desse mesmo ponto, tem um mínimo relativo em .
Resposta
(nenhum dos dois), (mínimo)