25-32 Use a derivada dada para encontrar todos os pontos críticos de e, em cada um deles, determine se ocorre um máximo relativo, um mínimo relativo ou nenhum desses. Suponha, em cada caso, que seja contínua em toda parte.

30.

Agora, o que nos resta é igualar a nossa função a zero. Assim, vamos ter

ou

Nós já achamos os nossos pontos críticos. O próximo passo é aplicar o teste da primeira derivada. Para isso, a gente vai precisar estudar o sinal da nossa função antes e depois dos nossos pontos críticos. Eu acho que isso vai ficar mais fácil com o auxílio de uma tabela. Então, bora lá.

Mas você deve estar aí se perguntando: ‘Caramba, como eu vou saber o comportamento dessas funções estranhas?’ Calma aeeeee. Vem comigo que vai dar certo.

Primeiro vamos analisar o A primeira coisa que deve estar passando pela sua cabeça é que se parece com a função de segundo grau Posso dizer uma coisa ??? Você está coberto de razão. O gráfico dessa função se parece muito com uma parábola ‘achatada’. Isso porque, para valores muito pequenos, o resultado é muito próximo de zero. Já para muito grande, ela assume valores maiores que os de . Por isso, ela cresce mais rapidamente do que a nossa função quadrática e está mais próxima do eixo . Então, se a função é positiva em todo o seu domínio, também vai ser, pois o seu expoente também é par.

Uma já foi. Ufa!!!! E nem foi tão difícil, viu?! No caso de perceba que se trata de uma função exponencial crescente, pois , deslocada três unidades para baixo sobre o eixo .

Tá complicado visualizar? Então olha só:

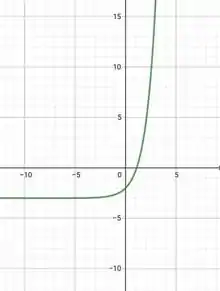
Ela é negativa antes de e positiva depois.

Nós já achamos os nossos pontos críticos. O próximo passo é aplicar o teste da primeira derivada. Para isso, a gente vai precisar estudar o sinal da nossa função antes e depois dos nossos pontos críticos. Eu acho que isso vai ficar mais fácil com o auxílio de uma tabela. Então, bora lá.

Agora que já montamos a nossa tabela, é só analisar os dados obtidos. Vem comigo!!!

Como à esquerda deé negativo e à direita também, não é extremo relativo. Já no caso do à sua esquerda é negativo e à sua direita é positivo. Portanto, ele é mínimo relativo.