Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.Revisão - Ex. 26
26.
- Dê as restrições sobre os domínios de que são impostas para fazer essas funções injetoras nas definições de .
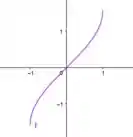
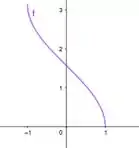
- Esboce os gráficos das funções trigonométricas restritas em e suas inversa.
Passo 1
As restrições nos intervalos dos domínios das funções em (a), são dados onde elas são contínuas, isto é, onde não encontramos nenhum salto, nenhum infinito no eixo y, ou alguma incoerência. Sabendo disso, temos que os intervalos são:
Então para as funções inversas, vamos ter que respeitar esses intervalos em cada domínio, logo:
Passo 2
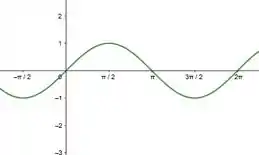
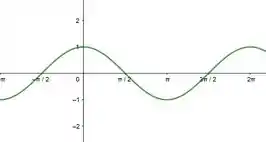
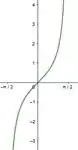
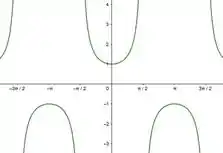
Os gráficos das funções trigonométricas em (a), são:
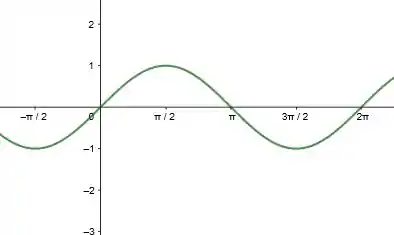
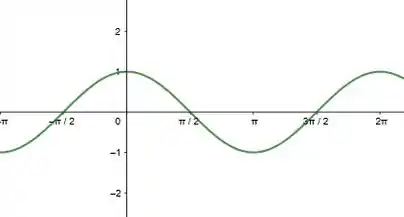
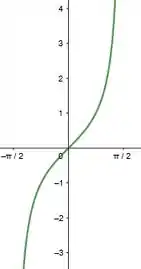
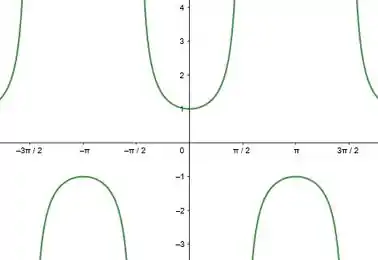
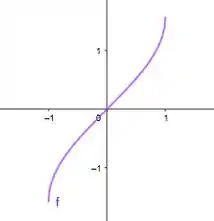
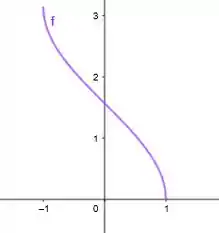
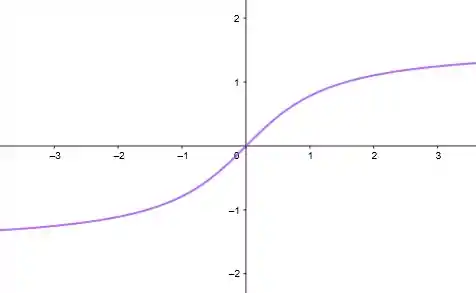
E suas inversas são:
Resposta
Dominios:
Gráficos:
Exercícios de Livros Relacionados
Encontre todos os valores de t no intervalo 0,2 π em que a equaçãos e n t = - 1 2 √ 2 está satisfeita.
Ache a t g ( θ ) se θ for o ângulo de inclinação entre as retas com as inclinações - 5 4 e - 7 5 .
Para que valores de t em [ 0 ,π ] temos c o t g ( t ) indefinida.
Ache, com aproximação de 1 grau, a medida do ângulo entre as retas com as inclinações - 3 2 e - 3 4 .
Defina a função fog e determine o seu domínio, para f x = s e c 1 x e g x = 1 ( x - π )