27. Um automóvel aproxima-se de um cruzamento a uma velocidade de . Quando o automóvel está a do cruzamento, um caminhão a uma velocidade atravessa o cruzamento. O automóvel e o caminhão estão em ruas que se cruzam em um ângulo reto. Com que velocidade o automóvel e o caminhão estarão se asfastando um do outro, s após o caminhão ter passado pelo cruzamento?
Passo 1
Beleza galera, a melhor forma de começarmos essa questão é imaginar a situação. Os carros tão num cruzamento como esse:
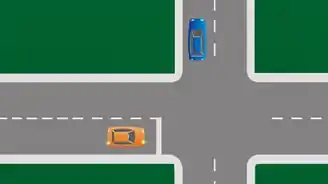
Uma boa forma da gente modelar isso é pensar num triângulo. Afinal, se os automóveis estão distantes em unidades e o cruzamento faz ângulos retos, podemos estabelecer o triângulo retângulo abaixo:
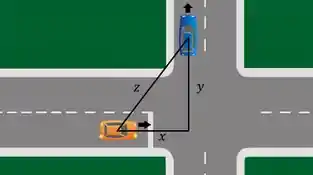
E conforme os carros se movimento, a distância deles muda! Beleza, próximo passo agora
Passo 2
Agora que entendemos a situação e nomeamos as variáveis, vamos voltar ao enunciado. Ele diz que o automóvel se aproxima do cruzamento a . Como quem está se aproximando do cruzamento é o carro laranja da figura, temos que:
Afinal galera, expressa a taxa de variação da posição com o tempo, que nada mais é que a velocidade. Show, resta agora a outra informação: “um caminhão a uma velocidade atravessa o cruzamento”. Na figura então, o caminhão está em azul e ele já passou o cruzamento, logo:
Dessas taxas a gente consegue, se mexer um pouquinho, chegar em expressões pra posição em função do tempo. Saca só:
Seguindo essa lógica:
Essas constantes atrapalham a gente, então vamos achar valores pra elas. Estabelecendo as coordenadas:
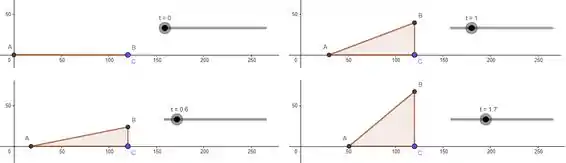
Onde é o automóvel laranja, é o automóvel azul e o ponto é o centro do cruzamento, vamso ter que:
E logo:
Guarda essas fórmulas que vamos acabar precisando delas
Passo 3
Beleza, é agora que vamos falar de taxas mesmo. Pra começar, como temos um triângulo retângulo, vale:
Show. Vamos derivar implicitamente em relação ao tempo então, já que taxas são derivadas! Pra isso, usamos a regra da cadeia e obtemos:
De Pitágoras de novo, fazemos:
Opa, achamos uma expressão para a taxa de variação da distância entre os automóveis! Pra um instante específico qualquer , daí, tiramos a expressão:
Passo 4
Chegamos no nosso último passo! Porque? Porque bem, dessa vez, sabemos o instante no qual queremos calcular a taxa! O enunciado diz: “[...] s após o caminhão ter passado pelo cruzamento?”. Logo, e teremos:
As taxas são constantes, não variando com o tempo, e já vimos elas:
Logo:
Agora, a gente tira do final do passo 2:
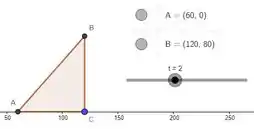
Ficando com: