Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.9 - Ex. 28
28. Uma corda está amarrada em um barco no nível da água e uma mulher em um cais puxa a corda a uma taxa de . Se as mãos da mulher estão a 5 m acima do nível da água, com que velocidade o bote estará se aproximando do cais, quando o comprimento da corda já puxada for de 6 m?
Passo 1
Um bom primeiro passo sempre é desenhar o problema pra entender! Ou então pegar uma imagem na internet hahaha
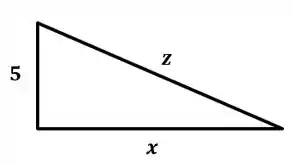
Pô, essa corda bem esticada aí, a gente sabendo a altura que as mãos da mulher estão em relação ao nível da água... porque não montar um triângulo retângulo? Vamos fazer isso então e aproveitar pra nomear variáveis:
Show, variáveis noemadas, partimos pro próximo passo que é relacionar elas.
Passo 2
Beleza galera, olha só, do nosso triângulo retângulo, se fizermos Pitágoras, achamos:
Variáveis relacionadas! Podemos partir agora pras taxas. Pra isso, basta derivar em relação ao tempo! E usando a regra da cadeia, derivando implicitamente, temos:
Show, achamos uma fórmula pra velocidade de aproximação do bote , o que é exatamente o que a questão quer saber. Perceba que ela depende somente da velocidade que a corda é puxada e do comprimento da corda . Para um instante qualquer , temos:
Passo 3
Ultimo passo galera! Mesmo a gente não sabendo em qual instante tudo isso acontece, do enunciado, sabemos que a mulher puxa a corda a uma taxa de e que a questão quer saber com que velocidade o bote estará se aproximando do cais, quando o comprimento da corda já puxada for de . Isso nos diz que:
Note que a taxa é negativa porque, se estabelecermos como origem do sistema os pés da mulher, percebemos que, ao puxar a corta, tanto o comprimento dela quanto a distância do barco pro cais diminui. Substituindo:
Perceba que a taxa negativa faz sentido, já que a distância do barco pro cais ta diminuindo.