Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.9 - Ex. 26
Uma certa quantidade de óleo está sendo despejado num tanque com a forma cônica invertida, a uma taxa de . Se o tanque tiver um raio de no topo e de profundidade, com que velocidade a profundidade do óleo estará quando ela estiver com de profundidade?
Passo 1
Taxas relacionadas pode parecer um pouco complicado, e as vezes é, pra ser sincero kkkk ;-; mas existe um passo a passo que pode nos ajudar muito pra resolver, confere ai:
1): ler bem o enunciado e anotar a informações necessárias.
2): fazer um lindo desenho para ilustrar o problema:
3): encontrar uma relação entre as variáveis, aqui vale tudo trigonometria, geometria, Pitágoras, Tales, lei dos senos, cossenos etc.
4): colocar toda a função em termos de uma única variável, aqui se aplica o mesmo que que no passo anterior, pode soltar a imaginação e a engenhosidade.
5): derivar a, manipular, substituir e zas e zas, aí você encontra a resposta.
Parece aqueles episódios do pateta tentando aprender alguma coisa kkk
Passo 2
Aqui estamos lidando com um cone com as seguintes dimensões, o raio vale , a altura é 10 e o volume aumenta em . O que queremos é, taxa de variação da altura quando a água estiver com 8 m de profundidade.
Anotando teremos:
(Raio do tanque)
(Altura do tanque)
(Taxa de aumento do volume)
(Queremos a tacha de variação da altura quando h=8(altura da óleo))
Passo 3
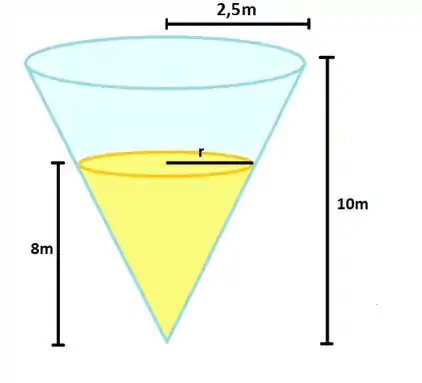
Agora é hora do desenho lindo :3
(raio da superfície da água) é uma variável assim como (altura da água), que vão depender do tempo, pois o volume da água aumenta com o passar do tempo.
Passo 4
Uma relação muito interessante para se usar aqui é a do volume do cone, veja como todas nossas variáveis aparecem nela.
Passo 5
Agora é hora de relacionar as variáveis, para que possamos derivar, para isso nós podemos simplificar a figura e pensar nela apenas vista de frente.
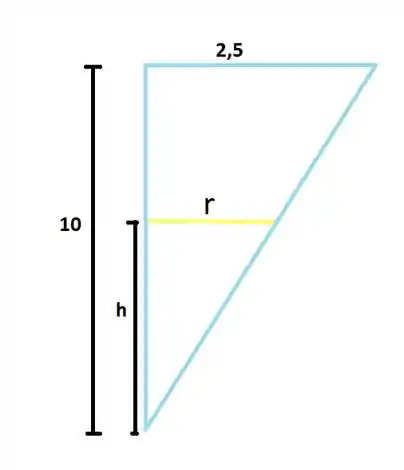
Lembrando dos tempos de escolinha podemos perceber que estes dois triângulos são semelhantes, pois o menor e resultado do corte do primeiro por uma reta paralela a um dos lados, com isso podemos montar a relação.
Nesse caso é interessante colocar a em função de , pois estamos interessados na variação da altura, além disso o valor de já foi informado.
Passo 6
Agora é hora de juntar as informações, derivar implicitamente, manipularmos a equação, substituir valores e zas e zas
Derivando implicitamente em relação a
Substituindo os valores:
Como as unidades estavam em metros e minutos a resposta será dada em metros e minutos
Ufaaa, pronto terminou, espero ter ajudado :3