Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.9 - Ex. 15
15. No exercício 14, com que velocidade a ponta da sombra do homem está se movimentando?
Passo 1
Vamos seguir os seguintes passos para resolver qualquer questão de taxas:
- Leia cuidadosamente o problema.
- Se possível, faça um diagrama.
- Identificar as variáveis e as constantes do problema.
- Escreva uma equação que relacione as variáveis.
- Derive em ambos os lados em relação a t usando regra da cadeia.
- Substituir o que foi dado e encontrar o que foi pedido.
Imagine a situação e faça um diagrama:
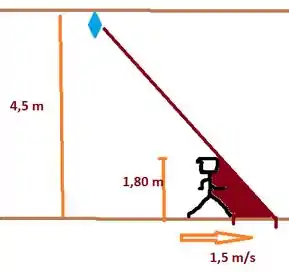
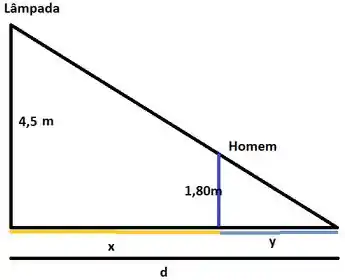
Variáveis:
x-Distância de quando a sobra estava sob o homem a posição atual do homem.
y- Tamanho da sombra.
d- Distância percorrida pela ponta da sombra.
t- tempo
Passo 2
Como queremos a velocidade de crescimento da ponta da sombra, queremos a taxa de variação de d (falou em velocidade e taxa de variação lembre-se de derivadas), e para isso precisamos encontrar uma expressão que relacione d. Lembrando que , observe o seguinte:
Passo 3
Agora que temos a equação que relaciona nossas variáveis. Vamos derivar implicitamente em relação a t, ou seja, vamos derivar em ambos os lados da igualdade em relação a t (pois estamos falando de velocidade).
Passo 4
Como x está se referindo à posição, será a velocidade, que é de . Assim, , ou .
Substituindo na equação do passo anterior, temos:
Logo, a velocidade de crescimento da ponta da sombra é de .