Exercícios de Taxa Relacionada – Casos Clássicos - Lista de Exercícios Resolvida
Questão 1
Dois navios a vapor estão navegando para longe de um ponto em rotas que forma um ângulo de . O navio desloca-se a 14 nós (milhas náuticas por hora). O navio desloca-se a 21 nós. A que taxa os navios estão se afastando entre si, quando e milhas náuticas?
Ver solução completaQuestão 2
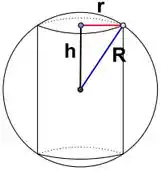
Um cilindro circular reto está inscrito em uma esfera. Se o raio da esfera cresce a uma taxa de e o raio da base do cilindro cresce a uma taxa de , com que razão está variando a área lateral do cilindro no momento em que o raio da esfera é e o raio da base do cilindro é de ?
Questão 3
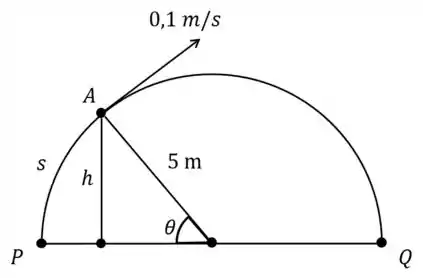
No desenho, o ponto representa um objeto que se desloca sobre uma semicircunferência de raio , com velocidade constante . Em cada instante, é a distância de até o diâmetro .
Durante o movimento de subida, qual será a taxa de variação da distância no momento em que ela medir ?
Questão 4
Um balão eleva-se verticalmente do solo à razão de . Quando o balão está a do solo, passa exatamente sob ele um automóvel viajando à velocidade de . Com que velocidade varia, segundos após, a distância entre eles?
Ver solução completaQuestão 5
Selecionado da Lista de Derivadas da Professora Renata - Cálculo 1 - UERJ
Um homem com de altura caminha em direção a um edifício, com uma velocidade de . Se existe um ponto de luz no chão a do edifício, com que velocidade a sombra do homem estará diminuindo, quando ele estiver a do edifício?
Ver solução completaQuestão 6
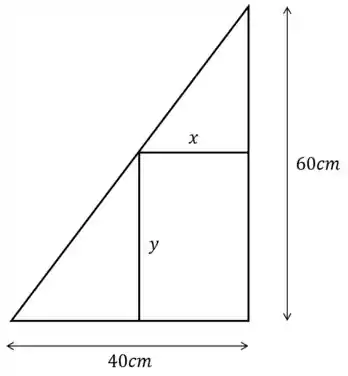
Um retângulo possui lados que variam com o tempo e está inscrito numa região triangular conforme a figura abaixo. Determine com que taxa a área do retângulo está variando no instante em que sua altura mede e está aumentando à taxa de . Neste instante a área está aumentando ou diminuindo?
Questão 7
Um holofote sobre o chão ilumina uma parede de m distante dele. Se um homem de m de altura anda do holofote em direção à parede a uma velocidade de m/s, quão rápido descreve o comprimento de sua sombra sobre a parede quando ele está a m dela?
Ver solução completaQuestão 8
Um velocista corre em uma pista circular de raio . Seu amigo está parado a uma distância de do centro da pista. Em um certo instante, quando a distância entre eles é de , o velocista está se afastando do amigo a uma velocidades de de volta por minuto. Quão rápido a distância entre os amigos está variando nesse momento?
Ver solução completaQuestão 9
(Enunciado adaptado em relação à prova original)
Considerando todos os trapézios regulares de área e tendo os seus menores ângulos internos valendo , calcule o menor valor possível de perímetro, nessas condições.
Ver solução completaQuestão 10
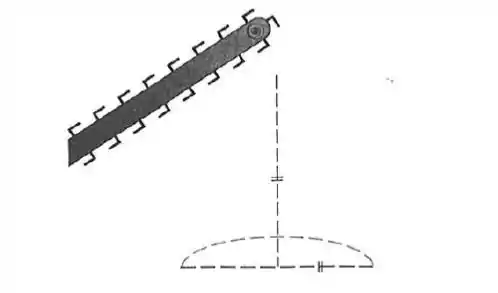
Uma esteira transportadora está descarregando cascalho de , constituindo uma pilha na forma de cone com o diâmetro da base e altura sempre igual. Quão rápido cresce a altura da pilha quando está a de altura?
Questão 11
Questão 4 - A superfície de um cubo oco, de aresta , é feita de um material que se encolhe uniformemente a uma taxa constante de . Determine com que taxa está diminuindo o volume do cubo no momento em que sua aresta mede .
Ver solução completaQuestão 12
Cascalho está caindo e formando uma pilha cônica que aumenta a uma taxa de , de modo que o raio do cone é sempre igual a sua altura. Encontre a taxa de variação da altura da pilha quando a altura é de .
Ver solução completaQuestão 13
Uma câmara de televisão no nível do solo está filmando a subida de um ônibus espacial que está subindo verticalmente de acordo com a equação , sendo a altura e o tempo. A câmara está a do local de lançamento. Encontre a taxa de variação da distância entre a câmara e a base do ônibus espacial, 10 segundos após o lançamento (suponha que a câmara e a base do ônibus estão no mesmo nível no tempo ).
Ver solução completaQuestão 14
O sol está se pondo com ângulo de elevação (ângulo entre os raios e uma reta horizontal) que diminui a uma taxa de radianos/hora. Com que velocidade estará crescendo a sombra de um prédio de metros de altura quando o ângulo de elevação do sol for ?
Ver solução completaQuestão 15
Uma escada de está encostada numa parede. Se a extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de , com que velocidade a extremidade superior estará descendo no instante em que a inferior estiver a da parede?
Ver solução completaQuestão 16
Uma roda gigante tem de raio e seu centro está a do solo. Ela gira no sentido anti-horário. Seja um ponto fixado nessa roda. No instante em que está a do solo, a distância de ao solo varia a uma taxa de .
A que taxa a roda está girando no instante ? (Ou seja, qual é a taxa de variação de em relação ao tempo no instante ?)
Do ponto parte um raio de luz que tangencia a circunferência e ilumina um ponto no solo. Qual é a taxa de variação da distância do ponto ao ponto que ele ilumina no solo no instante ?
Ver solução completaQuestão 17
Uma partícula se move sobre uma linha reta de modo que, no final de segundos, sua distância em metros do ponto de partida é dada por . Indique a velocidade da partícula no instante em que segundos:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 18
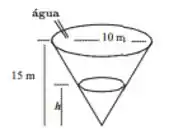
Enche-se de água um reservatório, cuja forma é de um cone circular reto (veja a figura), a uma taxa de . O vértice está a do topo e o raio do topo é de . Com que velocidade o nível da agua está subindo no instante em que ?
Questão 19
Considere o triângulo retângulo , em que os catetos são e . Assuma que e variam com o tempo e satisfazem a seguinte relação:
Num determinado instante , tem-se e a taxa de variação da área do triângulo é igual a .
Calcule a taxa de variação de no instante .
Calcule a taxa de variação do ângulo no instante .
Ver solução completaQuestão 20
Dois carros iniciam o movimento partindo de um mesmo ponto. Um viaja para o sul a e o outro para oeste a . A que taxa está crescendo a distância entre os carros duas horas depois?
Um carro A está se movimentando para o oeste a 90km/h e o carro B está se movimentando para o norte a 100 km/h. Ambos vão em direção à interseção de duas estradas. A que taxas os carros se aproximam um do outro quando o carro A está a 60 m e o carro B está a 80 m da interseção?
Ver solução completaQuestão 21
O período de um pêndulo simples é dado por:
Sendo L o comprimento do pêndulo, g a aceleração da gravidade e T é medido em segundos. Suponha que o comprimento do pêndulo é medido com um erro máximo de 0,5%. Qual a percentagem de erro máximo no período.
Ver solução completaQuestão 22
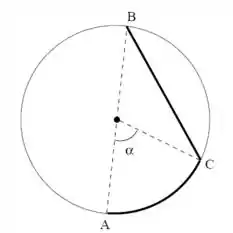
Para ir de um ponto a um ponto diametralmente oposto de uma piscina circular de de diâmetro, uma pessoa pode caminhar (com velocidade constante) pela borda da piscina até um ponto e nadar (com velocidade constante) em linha reta até o ponto (veja a figura).
Sabendo que ela pode caminhar vezes mais rápido do que pode nadar, determine, em termos de , as trajetórias que o levam ao seu destino no maior e no menor tempo.
(Obs.: Considere que ela pode somente caminhar ou somente nadar.)
Questão 23
Em uma fazenda de psicultura, uma população de peixes é colocada dentro de um lago e colhido regularmente. Um modelo para variação da população é dada pela equação:
Em que é a taxa de nascimento dos peixes, é a população máxima que o pequeno lago pode manter (capacidade de suporte) e é a porcentagem da população que é colhida.
Qual o valor de correspondente à população estável?
Ver solução completaQuestão 24
O raio de luz de um farol, que está situado a de uma praia reta, faz (rotações por minuto). Considere a altura do farol desprezível em relação a sua distância até a praia. Ache a velocidade da extremidade do raio de luz, ao longo da praia, quando ele faz um ângulo de com a linha da praia.
Ver solução completaQuestão 25
Da janela de um prédio, a metros do solo, um menino brinca com uma ponteira laser, movendo-a verticalmente e iluminando a parede do prédio vizinho, situado a uma distância de metros. Num determinado instante, o ponto de luz está a uma altura de metros e a velocidade com que ele sobe é de metros por segundo. Determine a taxa de variação do ângulo formado entre a horizontal e o feixe de luz nesse instante.
Ver solução completaQuestão 26
Uma esteira transportadora está descarregando cascalho de , constituindo uma pilha na forma de cone com o diâmetro da base e altura sempre igual. Quão rápido cresce a altura da pilha quando está a de altura?
Questão 27
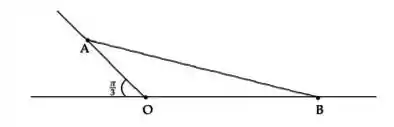
Uma barra, representada na figura pelo segmento , tem a extremidade apoiada em uma plano inclinado e a extremidade no chão conforme a figura. No instante a barra desliza de modo que o segmento mede e diminui a uma taxa de variação de s. Sabendo que o segmento mede no instante , determine a taxa de variação de neste instante.
Questão 28
Uma pedra caiu dentro de um lago, produzindo uma ondulação circular que cresce a uma velocidade radial de 60 m/s. Encontre a taxa segundo conforme a qual a área dentro do círculo está crescendo depois de a) 1s b) 3s c) 5s. O que você pode concluir
Ver solução completaQuestão 29
Dois carros iniciam o movimento de um mesmo ponto. Um viaja para o sul a 60 mi/h, e o outro para o oeste a 25 mi/h. A que taxa está crescendo a distância entre os carros duas horas depois?
Ver solução completaQuestão 30
A lei de Boyle estabelece que quando uma amostra de gás é comprimida a uma temperatura constante, o produto da pressão e do volume permanece constante:
Encontre a taxa de variação do volume em relação a pressão.
Ver solução completaQuestão 31
A lei de Boyle estabelece que quando uma amostra de gás é comprimida a uma temperatura constante, o produto da pressão e do volume permanece constante:
Uma amostra de gás está em um recipiente a baixa pressão e é regularmente comprimida a temperatura constante por 10 min. O Volume decresce mais rapidamente no início ou final dos 10 minutos. Explique.
Ver solução completaQuestão 32
Café está sendo derramado a uma taxa uniforme de em uma xícara em forma de cone truncado (ver figura abaixo). Se os raios superior e inferior da xícara forem de e e a altura for de , com que rapidez estará subindo o nível de café quando ele estiver na metade da xícara? [Sugestão: Estenda a xícara para baixo para formar um cone.]

Questão 33
Em uma fazenda de psicultura, uma população de peixes é colocada dentro de um lago e colhido regularmente. Um modelo para variação da população é dada pela equação:
Em que é a taxa de nascimento dos peixes, é a população máxima que o pequeno lago pode manter (capacidade de suporte) e é a porcentagem da população que é colhida.
Se o pequeno lago pode manter 1000 peixes a taxa de nascimento é 5% e a taxa de colheita é de 4%, encontre o nível estável da população.
Ver solução completaQuestão 34
Cristais de clorato de sódio são fáceis de crescer no formato de cubos permitindo uma solução de água e clorato de sódio evaporar vagarosamente. Se for o volume de cada cubo com comprimento de lado :
Calcule quando e explique seu signficiado.
Ver solução completaQuestão 35
Uma escada com 10m de comprimento está apoiada numa parede vertical. Seja o ângulo entre o topo da escala e a parede e a distância da base da escada até a parede. Se a base da escada escorregar para longe da parede, com que rapidez variará em relação a quando ?
Ver solução completaQuestão 36
Um cilindro circular reto está inscrito em uma esfera. Se o raio da esfera cresce a uma taxa de e o raio da base do cilindro cresce a uma taxa de , com que razão está variando a área lateral do cilindro no momento em que o raio da esfera é e o raio da base do cilindro é de ?
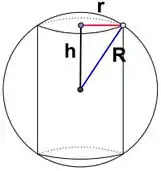
Questão 37
O raio de luz de um farol, que está situado a 3 km de uma praia reta, faz 8 rpm (rotações por minuto). Considere a altura do farol desprezível em relação a sua distância até a praia. Determine a velocidade da extremidade do raio de luz, ao longo da praia, quando ele faz um ângulo de 45° com a linha da praia.
Ver solução completaQuestão 38
Dois lados de um triângulo têm comprimentos fixos, e , respectivamente. O ângulo entre estes lados está crescendo à taxa de . Encontre a taxa segundo à qual a área do triângulo está crescendo quando o ângulo entre os lado de comprimento fixo é .
Ver solução completaQuestão 39
Enche-se de água um reservatório, cuja forma é de um cone circular reto, a uma taxa de 0,1 m³/s. O vértice está a 15 m do topo e o raio do topo é de 10 m. Com que velocidade o nível da água está subindo no instante em que h = 5 m?
Ver solução completaQuestão 40
Uma cisterna de de largura, de comprimento, de profundidade nas extremidades e no meio, de modo que o fundo seja formado por dois planos inclinados (veja a figura). Despeja-se água na cisterna a uma taxa de . Seja a altura do nível da água em relação à parte mais profunda. Com que velocidade (em metros por minuto) estará subindo no instante em que ?
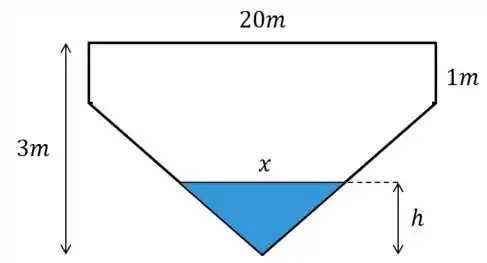
Questão 41
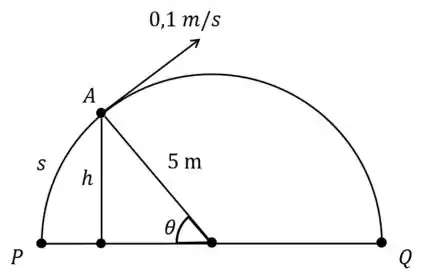
No desenho, o ponto representa um objeto que se desloca sobre uma semicircunferência de raio , com velocidade constante . Em cada instante, é a distância de até o diâmetro .
Durante o movimento de subida, qual será a taxa de variação da distância no momento em que ela medir ?
Questão 42
Uma escada de está encostada numa parede. Se a extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de , com que velocidade a extremidade superior estará descendo no instante em que a inferior estiver a da parede?
Ver solução completaQuestão 43
Uma escada de 8m está encostada numa parede. Se a extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de 2 m/s, com que velocidade a extremidade superior estará descendo no instante em que a extremidade inferior estiver a 3m da parede?
Ver solução completaQuestão 44
Um dos catetos de um triângulo retângulo diminui à uma taxa de , enquanto outro cresce . Em certo instante, o comprimento do primeiro lado é e o do segundo é . Passados , a que taxa está variando a área? Ela está aumentando ou diminuindo?
Ver solução completaQuestão 45
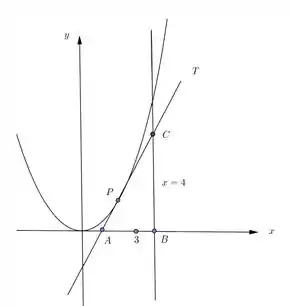
Considere a parábola .
I – Encontre a equação da reta tangente à parábola no ponto
II – Expresse a área do triangulo ABC em função de (ver figura).
III – Sabendo que o ponto parte da origem e que a taxa de variação da abscissa é , determine a taxa de variação da área do triângulo ABC, quando o ponto de tangência é .
Questão 46
Calcule a taxa de variação do volume de um balão esférico em relação ao seu raio, quando o raio do balão for igual a .
Ver solução completaQuestão 47
Suponha que o numero de indivíduos de uma população de bactérias seja dado no instante , por onde é uma constante e é a população inicial. Sabendo que a derivada da exponencial é ela própria, , resolva os itens seguintes.
- Determine o instante em que o número de indivíduos é metade do valor inicial
- Determine a derivada
- Determine a taxa de variação do número de indivíduos em relação ao tempo
- Sabendo que e , determine a taxa acima no instante calculado no item a)
Questão 48
Uma escada de está encostada numa parede. Se a extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de , com que velocidade a extremidade superior estará descendo no instante em que a inferior estiver a da parede?
Ver solução completaQuestão 49
Num determinado instante, um controlador de tráfego aéreo vê dois aviões na mesma altura voando a velocidades constantes, em trajetórias ortogonais que se cruzam num ponto (veja figura). Neste instante, um dos aviões está a 150 milhas do ponto e se aproxima de à milhas por hora, enquanto o outro está a milhas do ponto e se movendo à milhas por hora, também em direção ao ponto .
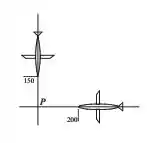
a) Antes do ponto a distância entre os aviões esta diminuindo? A que taxa?
b) Os aviões correm risco de choque? Em caso afirmativo, quanto tempo o controlador tem para fazer com que um dos aviões mude a sua trajetória?
Ver solução completaQuestão 50
Uma escada com 13 pés está em pé e apoiada em uma parede, quando sua base começa a
escorregar, afastando-se da parede. No momento em que a base está a 12 pés da casa, ela
escorrega a uma taxa de 5 pés/s.
(a) A que taxa o topo da escada escorrega para baixo nesse momento?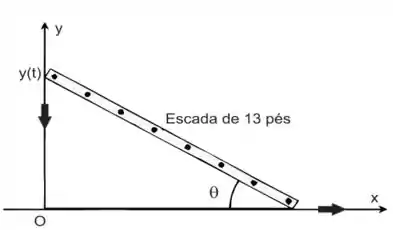
Questão 51
Uma escada com 13 pés está em pé e apoiada em uma parede, quando sua base começa a
escorregar, afastando-se da parede. No momento em que a base está a 12 pés da casa, ela
escorrega a uma taxa de 5 pés/s.
(b) A que taxa a área do triângulo, formado pela escada, parede e pelo solo, varia?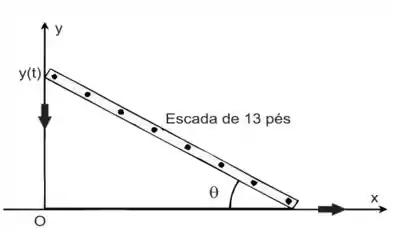
Questão 52
Uma escada com 13 pés está em pé e apoiada em uma parede, quando sua base começa a
escorregar, afastando-se da parede. No momento em que a base está a 12 pés da casa, ela
escorrega a uma taxa de 5 pés/s.
(c) A que taxa o ângulo, formado pela escada e pelo solo, varia?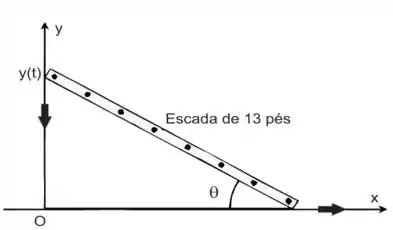
Questão 53
A área de um quadrado está crescendo a uma taxa de por minuto. Quão rápido o tamanho do lado do quadrado cresce quando ?
Ver solução completaQuestão 54
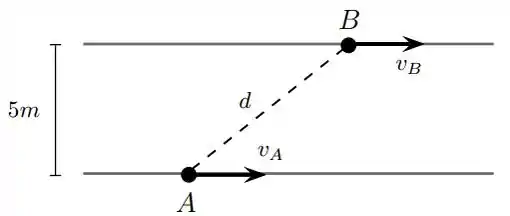
Dois caminhos retilíneos paralelos distam de metros . Os objetos e deslocam-se sobre os caminhos com velocidades e , respectivamente. Em um certo instante , a distancia entre eles é de , tem velocidade e tem velocidade , conforme a figura. Determine , a velocidade com que eles estão se aproximando.
Questão 55
Em uma fazenda de psicultura, uma população de peixes é colocada dentro de um lago e colhido regularmente. Um modelo para variação da população é dada pela equação:
Em que é a taxa de nascimento dos peixes, é a população máxima que o pequeno lago pode manter (capacidade de suporte) e é a porcentagem da população que é colhida.
O que acontece se é elevado a 5%?
Ver solução completaQuestão 56
Cristais de clorato de sódio são fáceis de crescer no formato de cubos permitindo uma solução de água e clorato de sódio evaporar vagarosamente. Se for o volume de cada cubo com comprimento de lado :
Mostre que a taxa de variação do volume de cada cubo em relação ao comprimento da aresta é igual a metade da área da superfície do cubo.
Ver solução completa