Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.Exercícios práticos - Ex. 29
29. Bombeamento de um reservatório Um reservatório em forma de cone circular reto, apontando para baixo, com 20 pés medidos transversalmente no topo e com 8 metros de profundidade, está cheio de água. Quanto trabalho é necessário para bombear a água a um nível 6 pés acima do topo?
Passo 1
Primeiro vamos transformar as medidas que estão em pés para metro:
Nós podemos desenhar a seção transversal de cone, em um plano cartesiano, para facilitar nossas contas:
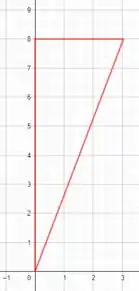
A reta que a lateral do cone faz é igual a
Passo 2
Imagine que esse reservatório é igual a uma soma de vários clindros com altura infinitesimais, cada clindros tem um volume de:
Mas, nós conhecemos a reta da lateral do cone, a coordenada dessa reta é igual ao raio, para cada valor de altura temos um raio, então:
O peso desse pedacinho de volume é igual ao voluma vezes a densidade da água, :
Passo 3
Para nós levarmos esse peso até o topo vamos ter que fazer um poquinho de trabalho, podemos escrever assim:
A altura que cada pedaço de volume subiu vai ser igual a menos sua própria altura:
Então seu trabalho é igual a
Passo 4
Integrando essa equação, vamos descobrir o trabalho total necessário para bombear a água: