Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.4 - Ex. 5

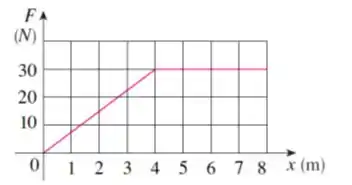
A figura a seguir mostra o gráfico de uma função força (em newtons) que cresce até seu máximo valor e depois permanece constante. Quanto trabalho é realizado pela força ao mover um objeto a uma distância de m?

Passo 1

E aí, galerinha! 😉

Nesse problema foi dado um gráfico de uma força com relação ao deslocamento e nosso objetivo é obter o trabalho que tal força realizou.

Tem ideia do que fazer? 🤔

Quando dizemos que o trabalho é a integral da força em função do deslocamento no intervalo que se interessa o deslocamento, estamos falando justamente da área do gráfico que corresponde ao trabalho.

Então, para encontrar o trabalho feito nessa situação, vamos achar a área entre a curva e o eixo .

Veja só! 😉

Passo 2

Temos uma área formada por um triangulo de base e altura e um retângulo de mesma base e altura, então, a área do gráfico é:

Logo, o trabalho que corresponde a essa área é dado por:

Legal, né? Responde Aí! 😁

Resposta

O trabalho realizado é de Joules.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

9) De acordo com a lei da gravitação de Newton, a Terra (massa M ) atrai uma partícula de massa m com uma força de intensidade ( G é a constante gravitacional) f r = G M m r 2 Onde r é a distância da

13) A B de constate k está presa ao suporte A e a um corpo de massa m . O comprimento normal da mola é l . Desprezando o atrito entre o corpo B e a barra horizontal, mostre que a aceleração a do corpo

Sobre uma partícula que se desloca sobre o eixo Ox atua uma força F → de intensidade 3N e que forma com o eixo Ox um ângulo x radianos.Calcule o trabalho realizado por F → quando a partícula se desloc

3) Uma partícula de massa m=1 desloca-se sobre o eixo O x sob a ação da força resultante F → x =- xi → . Sabe-se que no instante t = 0 a partícula encontra-se na posição x = 1ev = 2 . Verifique que, p

6) Uma partícula de massa m desloca-se sobre o eixo O x com aceleraçãoa , de sorte que a força resultante sobre a partícula é, pela Lei de Newton, m ai → . Sejam x 0ev 0 a posição e a velocidade no in