Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.10 - Ex. 29.c

29.Dadas as funções f ( x ) = x^2 - 1 e g ( x ) = 2 x - 1 :

( c ) Construa os gráficos de f ( x ) e g ( x ) .

Passo 1

Para fazer os gráficos, temos que lembrar qual a curva de uma função do 2 ° grau e do 1 ° grau.

Do 1 ° g r a u é uma reta.

Do 2° grau é uma parábola.

Passo 2

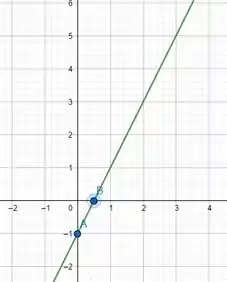
Vamos fazer o gráfico da reta, que é mais fácil, temos que determinar dois pontos, pois dois pontos determinam uma reta!

Para y = 0 , temos:

0 = 2 x - 1

1 = 2 x

x = (1)/(2)

Agora vamos para x = 0 :

g ( 0 ) = 2 (0) - 1

g ( 0 ) = - 1

Pronto, temos dois pontos e com isso determinamos a reta!

Os pontos A ( 0 , - 1 ) e B ((1)/(2) , 0)

Passo 3

Agora vamos para o gráfico de f ( x ) , é uma parábola com a > 0 , então concavidade para cima e quais são as raízes de f ( x ) ?

Ora, igualamos f ( x ) a 0 :

0 = x^2 - 1

1 = x^2

x = 1 ou x = - 1

Já temos duas raízes e sabemos a concavidade, já seria o bastante para desenharmos o gráfico, porém vamos descobrir em qual ponto a parábola corta o eixo y .

Para isso faremos x = 0 :

f ( 0 ) = ( 0 )^2 - 1 = - 1

Desenhando o gráfico com esses pontos em destaques, temos:

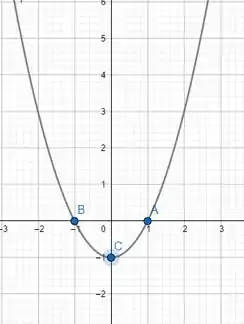
Resposta

f ( x )

g ( x )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual é o domínio natural de um polinômio?
Classifique cada equação como polinomial, racional, algébrica ou não uma função algébrica.(a) y = x + 2 (b) y = 3 x 4 - x + 1 (c) y = 5 x 3 + cos ⁡ 4 x (d) y = x 2 + 5 2 x - 7 (e) y = 3 x 2 + 4 x - 2
O gráfico de y = A s e n ( B x ) tem amplitude _______ e é peródico de período _______.
(a) Encontre uma equação para a família de retas cujos membros têm inclinação m = 3 .(b) Encontre uma equação para o membro da família que passe por ( - 1,3 ) .(c) Esboce os gráficos de alguns membros
Encontre uma equação para a família de retas cujos membros são perpendiculares àqueles do Exercício 1.