Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.3 - Ex. 1
(a) Encontre uma equação para a família de retas cujos membros têm inclinação .
(b) Encontre uma equação para o membro da família que passe por .
(c) Esboce os gráficos de alguns membros da família e marque-os com suas equações. Inclua a reta da parte (b).
Passo 1
(a) A equação da família das retas é desse tipo:
Onde é a inclinação (coeficiente angular) e é o coeficiente linear (onde corta o eixo ). Logo, se queremos :
Prontinho!
Passo 2
(b) Dentro da família de (a), isso é:
Queremos um membro que passe por , então, vamos substituir esse ponto na equação da reta:
Opa, então esse membro será:
Passo 3
(c) Aqui, vamos esboçar várias retas da família de (a), incluindo a reta da letra (b):
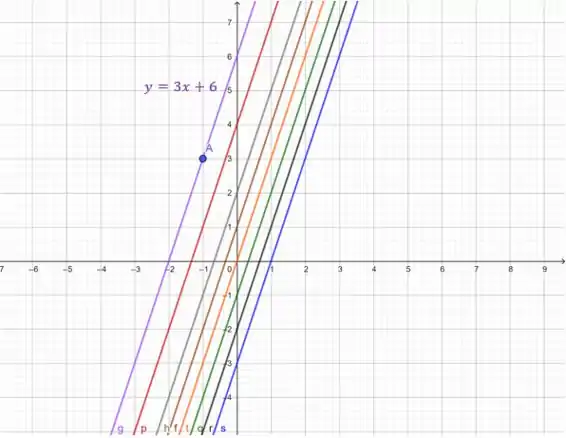
A reta de (b) está na figura! As outras são:
Resposta
(a)
(b)
(c)
Exercícios de Livros Relacionados
Classifique cada função como potência, função raiz, função polinomial (estabeleça seu grau), função racional, função algébrica, função trigonométrica, função exponencial, ou função logarítmica. d) y =
Classifique cada função como potência, função raiz, função polinomial (estabeleça seu grau), função racional, função algébrica, função trigonométrica, função exponencial, ou função logarítmica. c) h s
A tabela dá as alturas dos vencedores do salto com vara nas olímpiadas de 2004 . Faça um diagrama de dispersão e decida se um modelo linear é apropriado
A tabela dá as alturas dos vencedores do salto com vara nas olímpiadas de 2004 . d) É razoável usar o modelo pra predizer a altura vencedora de 2100?
A tabela dá as alturas dos vencedores do salto com vara nas olímpiadas de 2004 . b) Encontre e faça um gráfico de regressão.