Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.7 - Ex. 32
31-34 Verdadeiro/Falso Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta [No exercício 34, suponha que o quadrado girado fique no plano direitado eixo
32. O centroide de um losango é a interseção das diagonais do losango
Passo 1
Vamos começar a desenhando o gráfico esse losango.
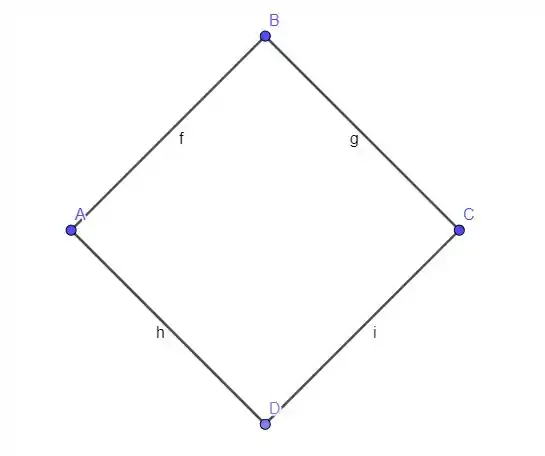
Passo 2
Precisamos traçar uma diagonal e ver se ela divide esse losango em duas partes simétricas, vamos fazer a diagonal primeiramente!
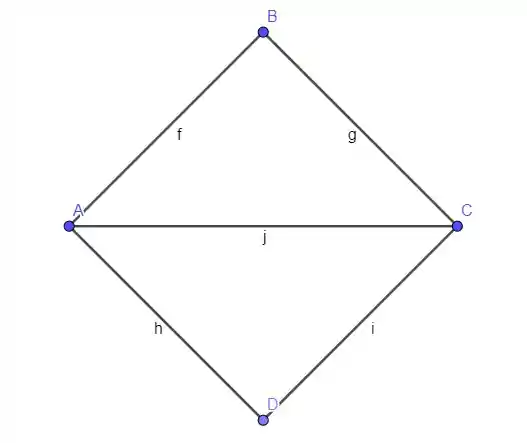
O triângulo ABC é igual ao triângulo ADC.
O retângulo é simétrico em relação a diagonal ! A diagonal é uma reta de equilíbrio, mas o que isso quer dizer?
Quer dizer que o centroide está no segmento AC.
Passo 3
Vamos fazer a mesma coisa só que para a diagonal , vamos lá:
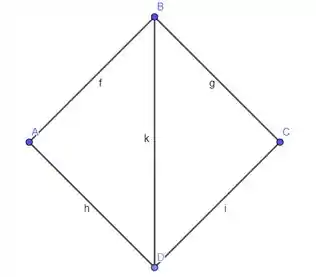
Olha lá! O losango também é simétrico em relação a diagonal , então a reta é uma reta de equilíbrio.
Afirmando tudo isso, podemos dizer que o centroide do losango está na diagonal .
Opaaaaa! O centroide está na diagonal e também está na diagonal , então o centroide tem de estar, não tem outra opção, no encontro dessas duas diagonais!!