Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.7 - Ex. 34
31-34 Verdadeiro/Falso Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta [No exercício 34, suponha que o quadrado girado fique no plano direitado eixo
34. Girando um quadrado em torno de seu centro, é possível mudar o volume do sólido de revolução obtido girando o quadrado em torno do eixo .
Passo 1
Nessa questão, calcularemos primeiro o volume do sólido de revolução em torno do eixo e depois giraremos o quadrado em torno do seu centro e calcularemos o volume do sólido de revolução em torno do eixo !
Após isso, compararemos esses dois volumes.
Vamos começar a desenhando o primeiro quadrado, o centroide é o ponto .
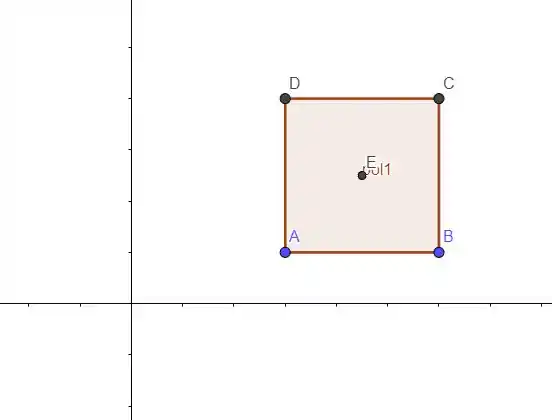
A distância entre o centroide e o eixo vamos chamar de .
Passo 2
Vamos fazer a rotação em torno do eixo agora e utilizar o teorema de papus para calcular o volume.
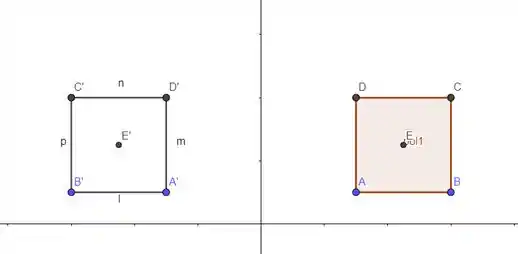
A distância percorrida pelo centroide é igual a . Lembrando que é a distância entre o centroide e o eixo e quando você rotacional, você está formando uma circunferência
Utilizando o Teorema de Papus, temos:
Em que é a área do quadrado!
Passo 3
Agora vamos rotacionar o quadrado em torno do centroide e desenhar a sua rotação em torno do eixo :
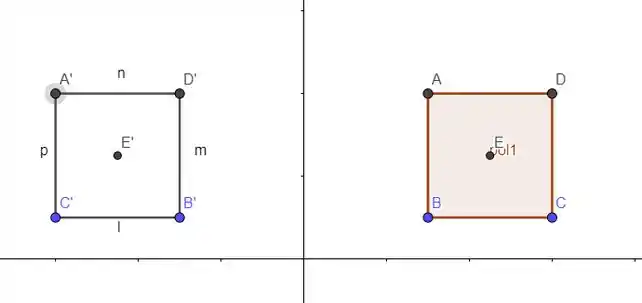
Ora, o centroide vai deslocar o mesmo comprimento se fizermos pelo quadrado antigo ou novo! E além disso, esses quadrados vão ter a mesma área!
Lembrando do Teorema de Papus, temos:
Como as áreas e as distância percorridas são iguais, podemos afirmar que os volumes das duas figuras rotacionadas são iguais também!
Então, não é possível mudarmos o volume da figura, apenas rotacionando o quadrado em torno do centroide, teríamos que transladá-lo. O que nos mostra que essa afirmativa é falsa.