Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.3 - Ex. 32
32. Se denota a reação do corpo para algum estímulo de intensidade , a sensitividade é definida como a taxa de variação de reação em relação a . Um exemplo acontece quando a luminosidade de uma fonte de luz é aumentada e o olho reage decrescendo a área da pupila. A fórmula experimental
Tem sido usada para modelar a dependência de em quando é medido em milímetros quadrados e em uma unidade de apropriada de luminosidade.
- Encontre a sensitividade
- Ilustre a parte (a) fazendo o gráfico de e como funções de . Comente sobre os valores de e em baixos níveis de luminosidade. Isso é o que você espera?
Passo 1
Olá, meu amigo. Vamos juntos resolvermos essa atividade.
Aqui, nos é pedido para encontrarmos a sensibilidade, depois de nos passarem a informação sobre a sensibilidade ser a taxa de variação de reação em relação a . Temos que a reação é dada por:
Como a sensitividade é a taxa de variação, teremos que fazer a derivada, pois taxa de variação nada mais é do que a derivada da função em relação a variável.
Usaremos a fórmula de divisão de derivada, pois temos aqui uma divisão de funções. Vou colocá-la aqui para facilitar nosso trabalho!
Para ilustramos os gráficos vamos utilizar o GeoGebra, um software matemático gratuito.
Passo 2
Vamos separar as funções assim fica mais claro:
Derivando o polinômio:
Utilizando a regra de derivação para polinômios:
Derivando o polinômio:
Utilizando a regra de derivação para polinômios:
Agora substituindo na expressão, temos:
Realizando os produtos:
Simplificando os termos semelhantes:
Encontramos a sensitividade! Agora vamos para a próxima!
Passo 3
(b)Gerando no software os gráficos:
Em vermelho o gráfico de e em Azul o de :
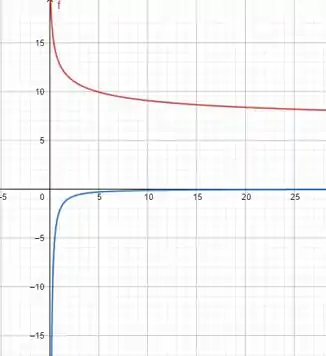
Para uns valores de luminosidades próximos de , temos que tende a , como é o decrescimento da pupila, acontece o que esperávamos, pois quando a luminosidade é baixa a pupila tende a não dilatar.
Para uns valores de luminosidades próximos de , temos que tende a , como é a taxa de variação que a pupila dilata, acontece o que esperávamos, pois quando a luminosidade é baixa a pupila tende a não dilatar.
Resposta
(a)
(b)
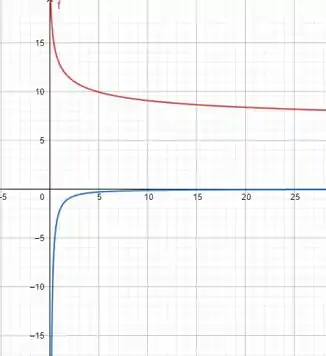
Para um valores de luminosidade próximos de , temos que tende a , como é o decrescimento da pupila, acontece o que esperávamos, pois quando a luminosidade é baixa a pupila tende a não dilatar.
Para um valores de luminosidade próximos de , temos que tende a , como é o taxa de variação que a pupila dilata, acontece o que esperávamos, pois quando a luminosidade é baixa a pupila tende a não dilatar.