Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.7 - Ex. 62
Se , faça os gráficos de e . Em quais intervalos ? Nesses intervalos, como está relacionado o gráfico de e suas retas tangentes? O que acontece nos intervalos onde ?
Passo 1
E aí! tudo certinho?
Nesse problema foi dada a função
E nosso objetivo é obter e para plotar seus gráficos utilizando uma ferramenta gráfica.
A partir desses gráficos e das funções obtidas, temos que dizer em quais intervalos e como esses intervalos estão relacionados com e suas retas tangentes. Além disso temos que dizer o que acontece quando .
Parece complicado?
Nesse caso, é uma função polinomial, então para calcular suas derivadas vamos utilizar a regra da potência
A partir da função que vamos obter, fazemos e encontramos os intervalos de que satisfazem a inequação.
E por fim, usamos a teoria para relacionar e .
Bora lá!
Passo 2
Vamos derivar a função duas vezes para obter , e então representar os gráficos usando um programa de computador.
Para a primeira derivada, teremos:
Derivando novamente:
Plotando os gráficos de e usando uma ferramenta gráfica, temos
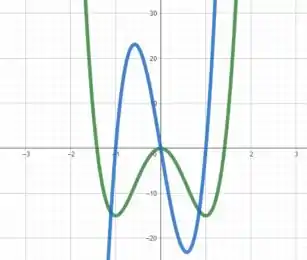
Em verde temos e em azul .
Tranquilo até aqui?
Passo 3
Agora vamos descobrir os intervalos onde .
Como vimos no passo 1, fazemos e observamos quais valores de satisfazem a inequação
Perceba que se , tem que ser maior que , ou seja
Então para , se .
Vamos analisar agora de ...
Temos um produto de e , então se for negativo, tem que ser negativo tambem para que quando fizermos o produto entre eles, o resultado seja positivo.
Dessa forma, vemos que quando e
Bacana, não é?
Passo 4
Para relacionar os gráficos de e , temos que lembrar que a derivada de uma função representa a inclinação da reta tangente da curva em um ponto... mas e a segunda derivada? Bom... a segunda derivada é a “inclinação da inclinação” 👀
Podemos interpretar isso como a concavidade da curva. Ou seja, representa a concavidade da função .
Então, quando , a concavidade de é positiva e quando é quando a concavidade de é negativa.
E aí! entendeu tudo? Responde Aí!
Resposta
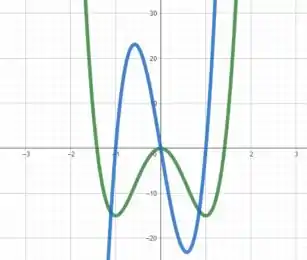
em verde e em azul.
quando e
respresenta a concavidade da curva