Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.2 - Ex. 32

Determine a massa e o centro de massa de um arame fino no formato de um quarto de círculo x 2 + y 2 = r 2 , x ≥ 0 , y ≥ 0 , se a função densidade for ρ x , y = x + y

Passo 1

E aiii turma, tudo bem!?

Nessa questão precisamos determinar a massa e o centro de massa de um arame fino que possui o formato de um quarto de círculo:

x 2 + y 2 = r 2 , x ≥ 0 e   y ≥ 0

Dado que a função densidade é:

ρ x , y = x + y

Tá, e agora?

Precisamos lembrar como é escrito em termos de integral a massa e o centro de massa.

A massa pode ser calculada pela seguinte integral de linha:

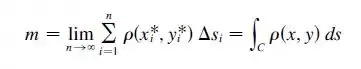
Já p centro de massa utilizamos as seguintes relações:

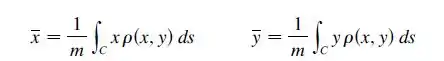
Agora quero que você repare no formato do fio. Veja que temos o formato de um circulo né, porem apenas no primeiro quadrante, onde:

x ≥ 0 e   y ≥ 0

Com isso podemos pensar em parametrizar em coordenadas polares, pois isso vai facilitar a resolução. Em coordenadas polares vamos ter:

x 2 + y 2 = r 2

x = r cos ⁡ t

y = r   s e n   t

Vamos chamar o ângulo de t ao invés de θ . Só para ficar mais com cara de parametrização mesmo, sem motivo especifico.

Por fim, lembre-se de mais uma coisa. Podemos reescrever a integral de linha também nesse formato:

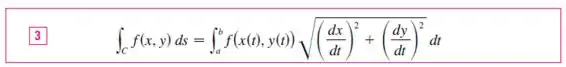
Agora ficou moleza ein! Só colocar mão na massa!

Vamos nessa!!!

Passo 2

Vamos começar calculando a massa.

Sabemos que o fio tem o formato de um círculo, apenas no primeiro quadrante, um quarto de círculo.

Por ser um círculo, podemos pensar na parametrização em coordenadas polares:

x 2 + y 2 = r 2

x = r cos ⁡ t

y = r   s e n   t

Como é um quarto e está no primeiro quadrante, temos que:

0 ≤ t ≤ π 2

Como eu sei que está no primeiro quadrante? Ele diz isso no enunciado da seguinte forma:

x ≥ 0 e y ≥ 0

Sabemos que a integral para calcular a massa é:

m = ∫ C ρ x , y d s

E que ρ x , y vale:

ρ x , y = x + y

Agora é só montar a integral.

Passo 3

Temos a seguinte integral:

m = ∫ C ( x + y ) d s

Agora vamos lembrar da nossa parametrização:

x = r cos ⁡ t

y = r   s e n   t

0 ≤ t ≤ π 2

Sabemos também que esse tipo de integral, ao parametrizar, vamos ficar com:

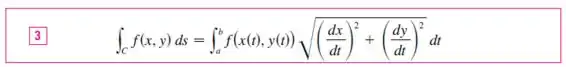
Repare que precisamos substituir x e y pela parametrização x ( t ) e y ( t ) , e aplicar suas derivadas em relação a t e substituir na raiz. Fazendo isso, temos que:

m = ∫ 0 π 2 r c o s   t + r s i n   t d d t r cos ⁡ t 2 + d d t r s e n ⁡ t 2   d t

Agora vamos derivar em relação a t e simplificar o máximo possível. Repare que dentro da raiz vai aparecer uma relação trigonométrica muito conhecida da qual vamos substituir:

cos 2 ⁡ x + s e n 2 ⁡ x = 1

Assim temos que:

m = ∫ 0 π 2 r c o s   t + r s i n   t r 2   d t

m = ∫ 0 π 2 ( r  cos ⁡ t + r  sin ⁡ t )   r   d t

Agora é só integrar, como r é uma constante em relação a d t podemos colocar para fora da integral, assim:

m = r 2 ∫ 0 π / 2 ( cos ⁡ t + sin ⁡ t )   d t

Integrando em d t , temos:

m = r 2 sin ⁡ t - cos ⁡ t 0 π 2

Aplicando os limites de integração:

m = r 2 1 - - 1

Logo, o valor da massa é:

m = 2 r 2

Passo 4

Agora vamos focar nas coordenadas do centro de massa.

Sabemos que as formulas são:

A ideia é parecida com o que fizemos para a achar a massa, vamos parametrizar tudo em função de t .

Aqui a gente pode polpar tempo, pois já sabemos do passo 3 que a massa vale:

m = 2 r 2

Que ρ x , y parametrizado é:

r c o s   t + r s e n   t

E que a raiz das derivadas ao quadrado é:

d d t r cos ⁡ t 2 + d d t r sen ⁡ t 2 = r

Vamos começar pelo centro de massa da coordenada x :

x - = ∫ x   ρ x , y   d s m

Substituindo os termos já parametrizados, temos que:

x - = 1 2 r 2 ∫ 0 π / 2 ( r   c o s   t )   ( r  cos ⁡ t + r  s e n ⁡ t )   d d t r cos ⁡ t 2 + d d t r sen ⁡ t 2   d t  

Simplificando um pouco conforme falamos acima, vamos ter:

x - = 1 2 r 2 ∫ 0 π / 2 ( r   c o s   t )   ( r cos ⁡ t + r sen ⁡ t )   r   d t  

x - = 1 2 r 2 ∫ 0 π / 2 r 3 c o s   t   (  cos ⁡ t + sen ⁡ t )     d t  

Como r é constate em relação a d t podemos colocar em evidência, assim:

x - = r 2 ∫ 0 π / 2 (   cos 2 ⁡ t + cos ⁡ t sen ⁡ t )     d t  

Passo 5

Precisamos resolver essa integral:

x - = r 2 ∫ 0 π / 2 (   cos 2 ⁡ t + cos ⁡ t sen ⁡ t )     d t  

Aqui vamos ter que aplicar uma relação trigonométrica para o cos 2 ⁡ t , da seguinte forma:

cos 2 ⁡ t = 1 + cos ⁡ 2 t 2

Fazendo isso temos:

x - = r 2 ∫ 0 π / 2 1 + cos ⁡ 2 t 2 + cos ⁡ t sen ⁡ t d t

Agora podemos separar esses termos, pois a integral de uma soma de termos é igual a soma da integral dos termos. Ficando assim:

x - = r 2 ∫ 0 π / 2 1 2 d t + ∫ 0 π / 2 1 2 cos ⁡ 2 t d t + ∫ 0 π / 2 cos ⁡ t sen ⁡ t d t

Vamos ter que aplicar duas substituições, do tipo:

u = 2 t

d u 2 = d t

v = s e n   t

d v = cos ⁡ t   d t

Substituindo temos que:

x - = r 2 ∫ 0 π / 2 1 2 d t + ∫ 0 π / 2 1 2 cos ⁡ u d u 2   + ∫ 0 π / 2 v d v

Integrando e voltando para a variável t , temos:

x - = r 2 1 2 t + 1 4 s e n   2 t + 1 2 s e n 2 t 0 π 2

Aplicando os limites de integração, temos:

x - = r 2 1 2 π 2 + 1 4 s e n   2 π 2 + 1 2 s e n 2 π 2 - 1 2 0 + 1 4 s e n   2 0 + s e n 2 0

x - = r 2 π 4 + 0 + 1 2 - 0 + 0 + 0

Simplificando, temos que o centro de massa em x vale:

x - = r [ π + 2 ] 8

Passo 6

Agora para a coordenada y do centro de massa:

y - = ∫ y   ρ x , y   d s m

A gente nem precisava calcular, pois pela simetria que a figura tem em relação ao eixo x e ao eixo y , tem que dar o mesmo valor. Mas vamos provar que isso é verdade.

Repare que comparando a expressão com o centro de massa em relação ao eixo x , a única diferença está no termo y que aparece multiplicando a densidade.

Logo podemos simplificar todas as etapas que foi feita no passo 5 e chegar na expressão:

x - = 1 2 r 2 ∫ 0 π / 2 r 3 s e n   t   (  cos ⁡ t + sen ⁡ t )     d t  

Agora vai ser o mesmo processo que fizemos para calcular o x - . Simplificando, temos que a integral é:

y - = r 2 ∫ 0 π / 2 ( sin ⁡ t cos ⁡ t + sin 2 ⁡ t )   d t

Aqui, vamos novamente utilizar uma relação trigonométrica. A seguinte:

sen 2 ⁡ t = 1 - cos ⁡ 2 t 2

Substituindo temos:

y - = r 2 ∫ 0 π / 2 ( sin ⁡ t cos ⁡ t + 1 - cos ⁡ 2 t 2 )   d t

Separando as integrais, vamos ter:

y - = r 2 ∫ 0 π / 2 1 2 d t - ∫ 0 π / 2 1 2 cos ⁡ 2 t d t + ∫ 0 π / 2 cos ⁡ t sen ⁡ t d t

Passo 7

Agora vamos utilizar substituições do tipo:

u = 2 t

d u 2 = d t

v = s e n   t

d v = cos ⁡ t   d t

Substituindo, isso nos dá:

y - = r 2 ∫ 0 π / 2 1 2 d t - ∫ 0 π / 2 1 4 cos ⁡ u d u + ∫ 0 π / 2 v d v

Integrando e votando a variável t , temos:

y - = r 2 1 2 t - 1 4 s e n   2 t + 1 2 s e n 2   t 0 π 2

Aplicando os limites de integração:

y - = r 2 1 2 π 2 - 1 4 s e n   2 π 2 + 1 2 s e n 2 π 2 - 1 2 0 - 1 4 s e n   2 0 + s e n 2 0

y - = r 2 π 4 - 0 + 1 2 - 0 - 0 + 0

Simplificando, temos que o centro de massa em y vale:

y - = r [ π + 2 ] 8

Viu, deu exatamente igual ao centro de massa em x , como tínhamos falado antes. Isso acontece devido a simetria da figura em relação aos eixos.

Resposta

m = 2 r 2

x - = y - = r [ π + 2 ] 8

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fio delgado é preso em dois suportes fixos de mesma altura, tomando a forma da catenária y = cosh ⁡ x ,- 2 ≤ x ≤ 2 . Supondo que a densidade do fio seja a mesma em todos os pontos, calcular a massa
Dado um arame semicircular uniforme de raio 4 cm.Mostrar que o momento de inércia em relação ao diâmetro que passa pelos extremos do arame 8 M , sendo M a massa do arame.
Dado um arame semicircular uniforme de raio 4 cm.Mostrar que o centro de massa está situado no eixo de simetria a uma distância de 8 π cm do centro.Mostrar que o momento de inércia em relação ao diâme
Calcular o momento de inércia em relação ao eixo dos z de uma espira da hélice circular uniforme: r ( t ) → = 2 cos ⁡ t i → + 2s e ntj → + t k →