Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.5 - Ex. 33
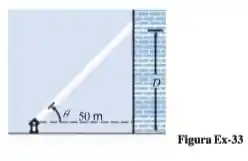
33- Um holofote lança um facho de luz sobre uma parede distante 50 m dele, conforme a figura abaixo. A distância entre o nível do chão e o local iluminado pelo facho na parede varia conforme o ângulo tomado pelo facho e a horizontal. Supondo que o holofote movimente o facho para cima e para baixo, encontre a taxa segundo qual a distância está variando com quando . Expresse sua resposta em metros/graus.
Passo 1
Galera, a primeira coisa que nós temos que fazer aqui é relacionar o e o .
Assim,
Bom... Se nós derivarmos o em relação ao , vamos achar a taxa de variação, certo ?
Dessa forma,
Passo 2
Caraaaaa, se você pensa que a questão acabou você se enganou, porque o exercício quer a taxa de variação em metros/grau.
Logo,
Fim !
Resposta
Exercícios de Livros Relacionados
19-24. Encontre d 2 y d x 2 .24. y = t gx
19-24. Encontre d 2 y d x 2 .22. y = x 2 . cos x + 4 s e nx
19-24. Encontre d 2 y d x 2 .23. y = s e nx . cos x
19-24. Encontre d 2 y d x 2 .21. y = x . s e nx - 3 cos x
19-24. Encontre d 2 y d x 2 .20. y = c o s s e cx