Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.5 - Ex. 33
33-34 Diz-se que uma função tem descontinuidade removível em se existe mas não é contínua em ou porque não está definida em ou porque a definição de difere do valor do limite. Essa terminologia será usada nestes exercícios.
33-a) Esboce o gráfico de uma função com uma descontinuidade removível em na qual não está definida.
b)Esboce o gráfico de uma função com uma descontinuidade removível em na qual está definida.
Passo 1
a)Galera, um bom exemplo para esse item é a seguinte função:
Essa função não está definida para , porém, para , podemos escrever . Logo,
Assim, temos um gráfico que é uma reta , sem o ponto
Bom, no nosso gráfico o ponto será o .
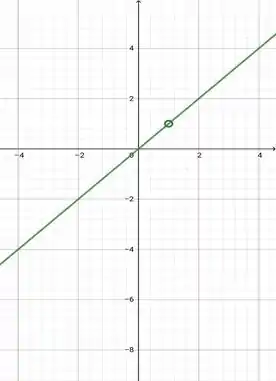
Passo 2
b) Galera, um bom exemplo para esse item é a seguinte função:
Essa função está definida para , mas é descontínua nesse ponto. Nesse caso a descontinuidade é removível. O gráfico é o mesmo do item a, acrescentando o ponto (será o pulinho no ).
O nosso ‘pulinho’ será no .
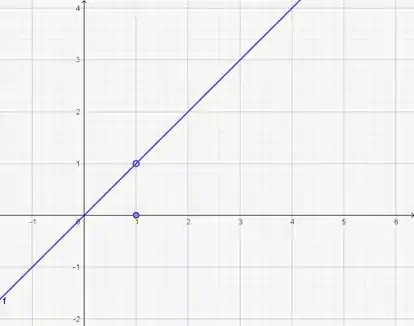
Resposta
a)Gráfico acima.
b)Gráfico acima.