Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.9 - Ex. 35

35. Dois caminhões aproximam-se de um cruzamento, um deles vindo da direção oeste e outro pelo sul. Se ambos estão com velocidade de k   k m / h , mostre que um se aproxima do outro com uma velocidade de k 2   k m / h , quando cada um está a m   k m do cruzamento.

Passo 1

Vamos seguir os seguintes passos para resolver qualquer questão de taxas:

  1. Leia cuidadosamente o problema.
  2. Se possível, faça um diagrama.
  3. Indentificar as variáveis e as constantes do problema.
  4. Escreva uma equação que relacione as variáveis.
  5. Derive em ambos os lados em relação a t usando regra da cadeia.
  6. Substituir o que foi dado e encontrar o que foi pedido.

Esquematizando o que está acontecendo :

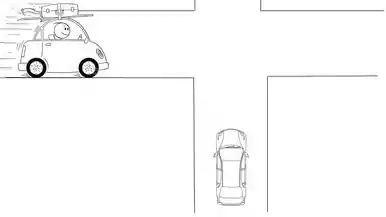
Se liga na dica, nessas questões você precisar ver um triângulo de algum modo.

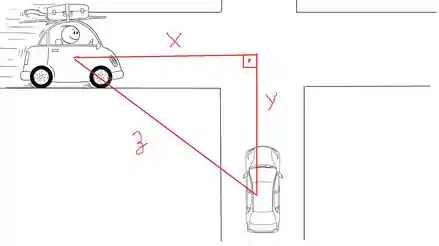
Pronto, agora fica bem mais fácil de resolver a questão.

Variaveis:

X – Distancia do automóvel na horizontal até o cruzamento.

y –Distância do automóvel na vertical até o cruzamento.

z- Distancia entre os carros.

Interpretando os dados que a questão deu:

d x d t = k   k m / h , essa é a velocidade do automóvel.

d y d t = k   k m / h , essa é a velocidade do caminhão.

Ele pede para provarmos que a taxa de variação da distância entre os dois veículos d z d t é k 2   k m / h   ,     quando cada um está a m km do cruzamento, ou seja, quando x e y forem iguais a m.

Passo 2

Precisamos encontrar uma fórmula que relacione as variáveis da questão, mas aí é muito simples, é só lembrarmos da fórmula do nosso conhecido Pitágoras:

  z 2 = x 2 + y 2

Passo 3

Já ilustramos o que a questão pediu, já encontramos a equação que descreve o problema, agora só falta derivar.

Derivando em ambos os lados em relação a t:

z 2 = x 2 + y 2

2 z d z d t   = 2 x d x d t + 2 y d y d t  

Isolando d z d t   ,

d z d t   = x d x d t + y d y d t z

Ops, conhecemos quase tudo, menos essse bendito z, então, voltaremos para fórmula de Pitágoras, a fim de descobri-lo.

z 2 = x 2 + y 2

Para x = m   e   y = m ,   temos:

z 2 = m 2 + m 2

z 2 = 2 m 2

z = 2 m 2 ⇒ z = m 2  

Voltando para as nossas derivas e substituindo o que já conhecemos:

d z d t   = m k + m k m 2

d z d t   = 2 k 2     × 2 2

d z d t   = 2 2 k 2    

d z d t   = k 2   k m / h

Provadinho, mas fácil do que você imaginava.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um meteorito entra na atmosfera da Terra e queima a uma taxa que, em cada instante, é proporcional à área de sua superfície. Supondo que o meteorito é sempre esférico, mostre que o raio decresce a uma
Uma partícula move-se ao longo da curva y= x x 2+1 . Encontre todos os valores de x nos quais a taxa de variação de x em relação ao tempo é três vezes a de y . [Suponha que d x / d t nunca é nula.]
A equação das lentes finas em Física é: 1 s + 1 S = 1 f onde s é a distância do objeto à lente, S é a distância da imagem à lente e f é a distância focal da lente. Suponha que uma certa lente tenha um
Resolva o Exercício 34 considerando a hipótese de que o ângulo entre as duas trajetórias de voo seja de 120 ° em vez de perpendicular. [Sugestão: Use a lei dos cossenos.]
Café está sendo derramado a uma taxa uniforme de 20c m 3 / s em uma xícara em forma de cone truncado (ver figura abaixo). Se os raios superior e inferior da xícara forem de 4 e 2c m e a altura for de