Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.4 - Ex. 47
Café está sendo derramado a uma taxa uniforme de em uma xícara em forma de cone truncado (ver figura abaixo). Se os raios superior e inferior da xícara forem de e e a altura for de , com que rapidez estará subindo o nível de café quando ele estiver na metade da xícara? [Sugestão: Estenda a xícara para baixo para formar um cone.]
Passo 1
Vamos começar já usando a dica que o enunciado dá, colocando os dados nos seus lugares e dando nome a alguns comprimentos, beleza?
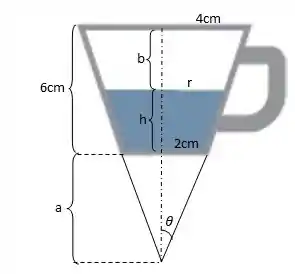
Agora podemos tirar algumas informações desse desenho. Olhando para a tangente do ângulo:
Logo
E além disso:
Passo 2
Como estamos interessados em relacionar o volume ocupado pelo liquido com as dimensões, vamos ter que falar que o volume do tronco de cone formado pelo líquido nada mais é do que o volume do cone de altura menos o volume do cone de altura
Mas , lembra?
Passo 3
Agora podemos substituir o valor de encontrado na equação (1) dentro da equação (2):
Abrindo esses termos:
Opa parece a expressão começou a ficar menos feia
Show de bola, agora temos uma expressão que depende apenas do volume e da altura do líquido, que são dados que interessam a gente.
Passo 4
Derivando essa expressão em relação ao tempo:
Pela regra da cadeia teremos:
Passo 5
Como o enunciado fala que o café é derramado a uma taxa uniforme de isso nos diz que:
E nos pergunta com que rapidez estará subindo o nível de café quando ele estiver na metade da xícara, queremos no instante em que
Substituindo todos esses dados na equação (3), teremos: