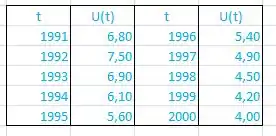
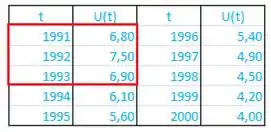
A taxa de desemprego varia com o tempo. A tabela (do Bureau of Labor Statistics) dá a porcentagem de desemprego na força de trabalho norte-americana de a .
- Qual o significado de Quais são suas unidades?
- Construa a tabela de valores de .
Passo 1
Fala galera!
Aqui temos uma tabela de valores de e precisamos de algumas informações sobre sua derivada:
- Seu significado
- Sua unidade
- Uma tabela com seus valores
Vamos começar lembrando que a derivada é uma taxa de variação de uma grandeza. Nesta situação, a derivada é a taxa de variação da taxa de desemprego em um dado momento. Em outras palavras, quanto tende a variar do ano em direção ao seguinte.
Vamos discutir mais isso no passo 2!
Pra calcular as derivadas, iremos supor que os números de desemprego não sofram uma variação violenta, pois assim conseguiremos calcular a tabela das derivadas.
A gente vai usar a definição de derivada que considera a derivada como a inclinação da reta tangente no ponto:
No entanto, sendo uma aproximação, nós também podemos usar outras 2 fórmulas pra calcular as derivadas assim. Nesta última consideramos um ponto de interesse e um outro ponto um pouco maior .
Na aproximação a seguir, consideramos o ponto de interesse e um ponto um pouco MENOR
E nessa última possibilidade, vamos considerar 2 pontos, um maior e outro menor que o nosso ponto de interesse:
Eu to te apresentando essas 3 formas de calcular, pois no primeiro e no último ano de que temos dados, vamos ter que fazer cálculos diferentes, por conta dos dados que temos disponíveis.
Agora vamos aos cálculos.
Passo 2
Respondendo a letra (a) então, é o tanto que a taxa de desemprego está variando no ano . Se ela é positiva, a tendência é que vamos ter mais desemprego. Se ela é negativa, quer dizer que o desemprego está caindo.
Sua unidade é a razão entre as unidades de e :
Agora vamos às derivadas!
Passo 3
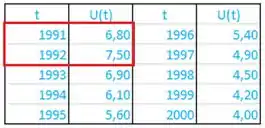
Pra calcular a derivada no ano de , nós não temos ponto antes, então não podemos fazer . Só temos o dado no ponto e dados depois, então só podemos usar essa fórmula aqui:
Que nas nossas variáveis, fica:
Vamos considerar que vai ser o ano de 1992, então e:
Passo 4
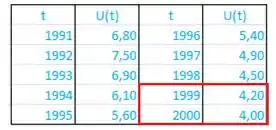
Pro ano de , nós só temos o valor no ponto e no anterior, então temos que usar essa fórmula aqui:
Que nas nossas variáveis fica:
Vamos considerar que vai ser o ano de 1999, então e:
Passo 5
Pra todos os outros pontos, nós temos o valor no ponto, no ano anterior e no ano seguinte. Então nós vamos usar a aproximação a seguir, que é mais precisa:
Nas nossas variáveis, fica:
Pro ano , vamos fazer:
Então a derivada nesse ponto fica:
Pra todos os outros pontos, vamos fazer o mesmo esquema, usar um ponto imediatamente anterior e um imediatamente posterior e usar essa mesma fórmula. Então vou ser mais sucinta nos cálculos a partir de aqui:
Pro ano
Pro ano
Vou repetir a tabela pra gente não ficar tendo que subir a tela:
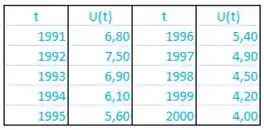
Pro ano
Pro ano
Pro ano
Pro ano
Pro ano
Ufa! Acabamos!
Passo 6
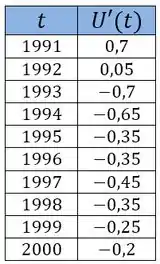
Juntando todas essas derivadas numa tabela, temos:
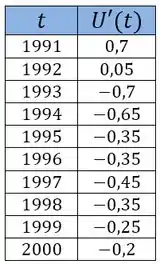
Resposta
o tanto que a taxa de desemprego está variando no ano .