24. A tabela mostra como a média de idade de idade das mulheres japonesas que se casam pela primeira vez variou na última metade do século XX

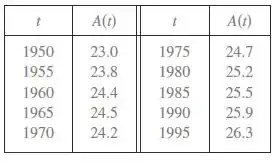
1. Use uma calculadora gráfica ou computador para modelar esses dados por um polinômio de quarto grau.
2. Use a parte (a) para achar modelo para A’(t)
3. Estime a taxa de variação da idade de primeiro casamento dessas mulheres em
4. Faça um gráfico dos pontos dados e os modelos para A e A’.

(b) Derivaremos .

(c) Para estimarmos a taxa de variação, antes colocaremos a fórmula da derivada!

Os menores valores de são e

Agora substituiremos :

Faremos agora a média entre esses dois valores para aumentarmos a precisão, porém como eles são iguais, podemos apenas repetir esses valores

(d) Nesse passo faremos esses três gráficos! Primeiro o dos pontos em preto e da modelagem em azul!

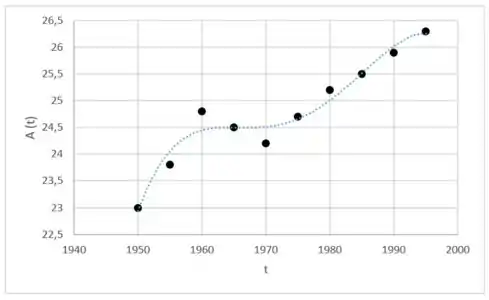
E por fim de A’(t):

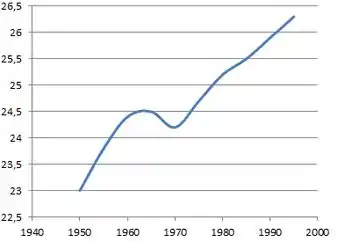
Prontinho!