Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.9 - Ex. 9
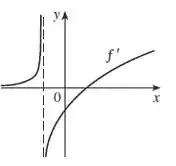
Trace ou copie o gráfico de . (Suponha os eixos com a mesma escala.) Use o método do Exemplo 1 para esboçar o gráfico de .
9.
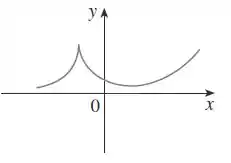
Passo 1
E aí, pessoal!
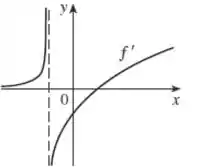
Nesse problema foi dado um gráfico de uma função e nosso objetivo é esboçar o gráfico de .
Antes de ver como resolvemos esse problema vamos dar uma olhada nesse gráfico...
Parece complicado?
Para resolver esse problema vamos analisar o comportamento da reta tangente da função ao longo do seu domínio.
Fazemos isso pois a inclinação da reta tangente da função em um ponto nada mais é do que a derivada da função naquele ponto.
Sacou? Bora começar!
Passo 2
Vamos começar para valores negativos no “começo” do gráfico...
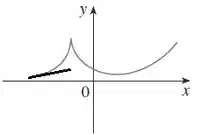
Na figura acima, vemos que a derivada é positiva, e pequena, porém com o crescimento de a inclinação da reta também aumenta!!
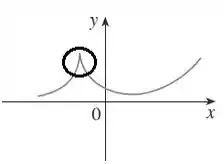
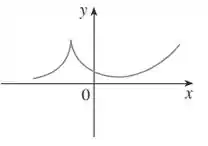
No ponto em que colocamos uma “lupa”, a derivada possui uma descontinuidade, pois ela contém um “bico”. Então perceba que no lado esquerdo do bico, a inclinação da reta tangente vai tender a pois a função está quase vertical. Já no lado direito a inclinação da reta tangente vai tender a pois decresce muito bruscamente.
Tranquilo até aqui?
Passo 3
Vamos continuar nossa análise... depois do bico temos
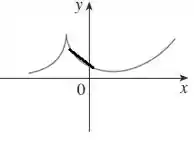
Perceba que a inclinação da reta tangente nessas proximidades é negativa, mas aumenta conforme aumenta.
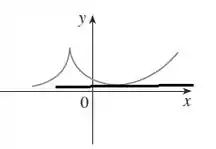
Até que em um momento a reta tangente é horizontal e sua inclinação é . Esse ponto é muito importante pois como a inclinação é , , então será um ponto onde a função corta o eixo .
Bacana, não é?
Passo 4
Por fim, temos que
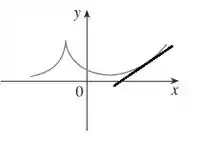
Depois que a função passa pelo ponto onde a inclinação é nula, a inclinação da reta tangente cresce e é sempre positiva.
Juntando todas as informações que obtemos até agora, temos que inicialmente a função é proximo de e aumenta exponencialmente até .
Nesse ponto há uma descontinuidade em que na direita a função tende a e cresce de forma amortecida.
E aí! entendeu tudo? Responde Aí!
Resposta
