Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 9.5 - Ex. 3
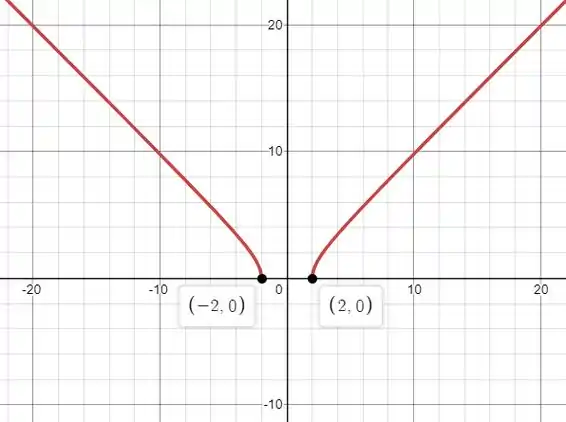
Esboce o gráfico.
Passo 1
Oi, pessoal! Tudo bom? Antes de começar a esboçar qualquer gráfico é importante a gente saber qual o domínio dele.
Como trata-se de uma raiz quadrada, temos uma restrição quanto ao argumento que só pode ser positivo, ou seja,
Logo, temos que o dominio é .
Agora vamos achar os intervalos de crescimento e decrescimento! Para isso derivar e fazer o estudo do sinal!
Passo 2
Vamos usar a regra da cadeia! Então temos que,
Lembrando que a derivada do polinômio e da função constante são:
Vamos então aplicar:
Ajeitando,
Passo 3
Agora vamos analisar o sinal de igualando a zero:
Temos que analisar o denominador também, evitando que ele seja nulo, assim:
Vamos analisar o sinal da expressão:
Para temos:
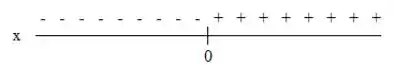
A expressão assume valores negativos quando e assume valores positivos quando .
Para temos:
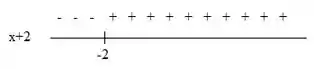
Aqui a expressão assume valores negativos quando e assume valores positivos quando .
Para temos:
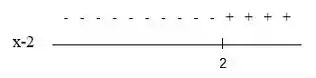
Aqui a expressão assume valores negativos quando e assume valores positivos quando .
Passo 4
Vamos lá, agora vamos analisar as duas imagens que achamos no passo anterior:
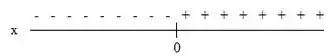
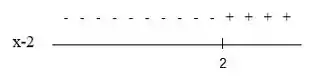
Temos que em:
Então é estritamente crescente em
E em:
Então é estritamente decrescente em
Lembrando que nos outros intervalos a função não é definida.
Passo 5
Vamos achar os pontos de inflexão e como se comporta a concavidade através de .
Para isso vamos usar mais uma regra, a da divisão:
Aplicando:
Derivando,
Ajeitando
Por fim,
Vamos analisar agora o sinal de onde o denominador não pode ser igual a :
em e , tendo a concavidade voltada para baixo.
Não há ponto de inflexão, pois não há uma mudança de concavidade.
Passo 6
Para esboçar o gráfico vamos calcular os limites de para e :
Passo 7
Pronto, agora podemos esboçar o gráfico juntando todas as informações. Ele fica assim:
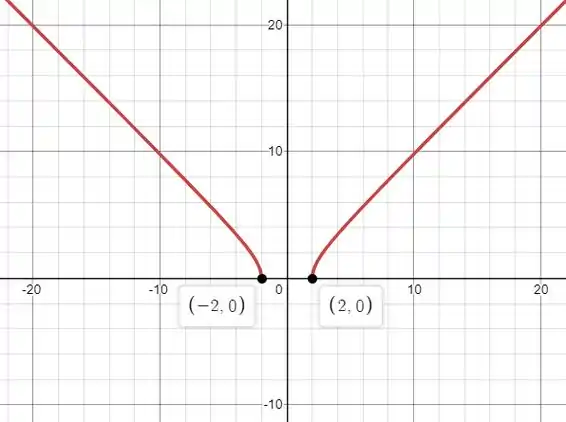
Resposta
