3.Em cada parte, esboce uma figura análoga à figura 5.6.10 para a região especificada. [Considere a fronteira superior da região. Se for único, identifique e no esboço. Caso contrário, identifique no esboço e determine todos os valores de que satisfazem a Equação (8).]
a) A região da parte (a) do Exercício .
b) A região da parte (b) do Exercício .
c) A região da parte (c) do Exercício .
Passo 1
Vou começar mostrando essa famigerada equação 8, que ele diz. É na verdade o Teorema do Valor Médio.
Basicamente, o que esse teorema diz é que existe uma função constante que tem área igual o valor da integral, é o mesmo conceito que você verá em Força Média!!
Vamos para a letra a), lembrando que queremos descobrir o .
Vamos calcular essa integral.
Retomando a expressão do teorema médio.
Então:
Já calculamos , agora precisamos saber qual é esse valor de .
Se , então:
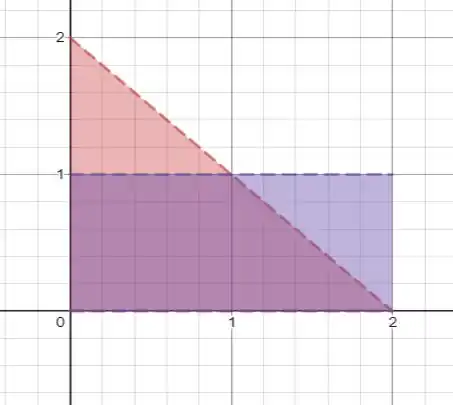
Para desenharmos o gráfico como na figura 5.6.10, temos que desenhar o gráfico da função e um retângulo de altura e de intervalo entre e .
Passo 2
Vamos para a letra b), lembrando que queremos descobrir o .
Vamos calcular essa integral.
Retomando a expressão do teorema médio.
Então:
Já calculamos , agora precisamos saber qual é esse valor de .
Só que é verdade para qualquer de entre e .
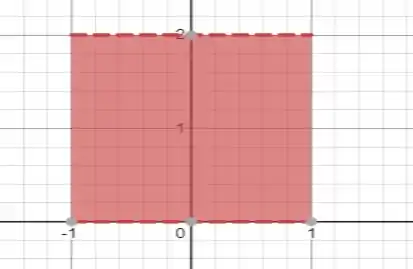
Para desenharmos o gráfico como na figura 5.6.10, temos que desenhar o gráfico da função e um retângulo de altura e de intervalo entre e .
Só que se você perceber, vamos desenhar dois gráficos iguais, então vou apenas desenhar uma vez.
Passo 3
Vamos para a letra b), lembrando que queremos descobrir o .
Vamos calcular essa integral.
Retomando a expressão do teorema médio.
Então:
Já calculamos , agora precisamos saber qual é esse valor de .
Se , então:
Para desenharmos o gráfico como na figura 5.6.10, temos que desenhar o gráfico da função e um retângulo de altura e de intervalo entre 1 e .
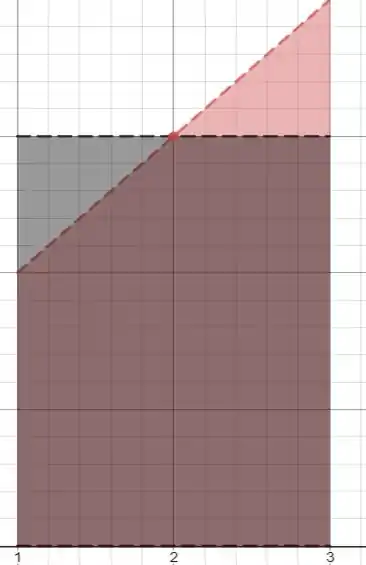
O ponto em vermelho é o valor médio.
Resposta
a)
b)
c)