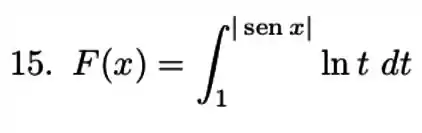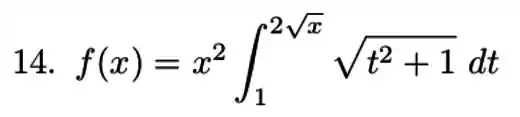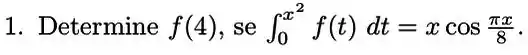Exercícios de Teorema Fundamental do Cálculo - Lista de Exercícios Resolvida
Questão 3
Seja
É dado que
- Determine
- Ache a área do triangulo limitado pelos eixos e pela reta tangente ao gráfico de no ponto .
Questão 9
Seja .
Calcule para .
Verifique se é derivável em . Em caso afirmativo, calcule .
Ver solução completaQuestão 16
Sejam e funções contínuas em tais que:
- Calcule:
- Calcule e , sendo definida por:
Questão 18
Considere a função
Determine os dois pontos críticos de , isto é, os pontos onde .
Identifique qual desses pontos é ponto de máximo e qual é ponto de mínimo. Justifique.
Ver solução completaQuestão 19
Seja definida por
Selecione a opção que apresenta os intervalos onde o gráfico da função é côncavo para baixo:
e
e
e
e
Ver solução completaQuestão 22
Sejam função diferenciável cuja derivada é contínua, tal que
O valor de da integral é:
Questão 26
Considere a função dada por
- Determine e .
- Calcule , utilizando o Teorema Fundamental do Cálculo.
Questão 27
Seja uma função contínua que satisfaz sendo uma constante não nula. O valor de é igual a:
- 4.
- 2.
- 1.
- 6.
- 0.
Questão 28
Seja uma função contínua que satisfaz sendo uma constante não nula. O valor de é igual a:
- 2.
- 4.
- 1.
- 6.
- 0.
Questão 29
Seja uma função contínua que satisfaz sendo uma constante não nula. O valor de é igual a:
- 2.
- 4.
- 1.
- 6.
- 0.
Questão 33
Considere:
Onde é a função cujo gráfico é dado abaixo:
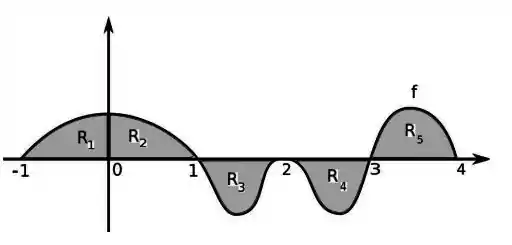
Sabendo que as áreas das regiões , , , e são:
, , , e .
Determine os pontos de máximo e mínimo local da função .
Ver solução completaQuestão 34
Considere definida por . Na figura abaixo, representa a área da região indicada e é a área do triângulo com vértices em , e indicado.
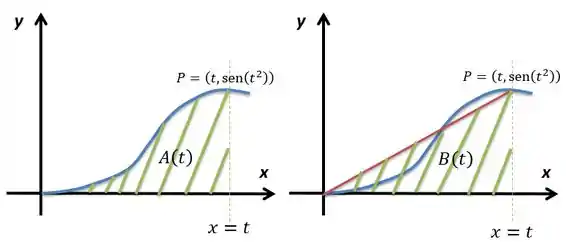
Determine .
Ver solução completaQuestão 35
Considere a função
Ache a equação da reta que é tangente ao gráfico de no ponto . Em seguida ache as coordenadas do ponto de interseção da reta com a reta dada por:
Ver solução completaQuestão 37
Sobre
é correto afirmar que :
- Seu valor é
- Seu valor é
- Seu valor é
- Seu valor é
- O limite não existe
Questão 40
Considere a função , definida por
,
Determine o valor de , sabendo que
Ver solução completaQuestão 41
Seja a função dada por
Determine, caso exista(m):
- e (a primeira e a segunda derivadas de ).
- O(s) intervalo(s) onde é crescente.
- O(s) intervalo(s) onde o gráfico de tem concavidade voltada para baixo.
Questão 45
Em cada item, utilize o Primeiro Teorema Fundamental do Cálculo, propriedades da integral (se necessário) e as regras de derivação (se necessário) para calcular a derivada da função :
Questão 46
ME04) Seja uma função contínua cujo gráfico está representado abaixo:
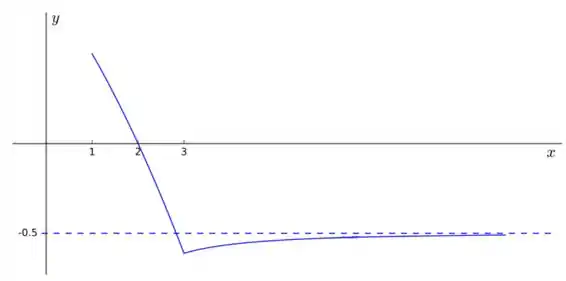
Considere as informações sobre a função:
Com :
- é crescente em e decrescente em
- é contínua, mas não é derivável
É correto dizer que:
- As afirmações e são verdadeiras
- Todas as afirmações são verdadeiras
- As afirmações e são verdadeiras
- Todas as afirmações são falsas
- As afirmações e são verdadeiras
Questão 49
Considere a função definida por
a) Determine a primeira e a segunda derivadas de .
b) Determine a abscissa (coordenada ) do ponto de inflexão do gráfico de . Justifique sua resposta.
c) Determine a ordenada (coordenada ) do ponto de inflexão do gráfico de . Justifique sua resposta.
Ver solução completaQuestão 54
Use o Teorema Fundamental do Cálculo para calcular a derivada da função
Justifique seu trabalho.
Ver solução completaQuestão 59
A função definida pela relação
tem dois mínimos locais nos pontos respectivamente.
O valor de é é:
Questão 60
Use o Teorema Fundamental do Cálculo para achar a derivada da função.
c)
Ver solução completaQuestão 61
Use o Teorema Fundamental do Cálculo para achar a derivada da função.
f)
Ver solução completaQuestão 62
Use o Teorema Fundamental do Cálculo para achar a derivada da função.
g)
Ver solução completaQuestão 64
-
Define a função onde f(x) é uma função definida por partes.
- Determine onde é diferenciável.
Questão 66
Se for uma função contínua tal que
Para todo , ache a fórmula para e calcule .
Ver solução completaQuestão 68
Use o Teorema Fundamental do Cálculo para achar a derivada da função.
Questão 69
Use o Teorema Fundamental do Cálculo para achar a derivada da função.
b)
Ver solução completaQuestão 70
Use o Teorema Fundamental do Cálculo para achar a derivada da função.
d)
Ver solução completaQuestão 71
Use o Teorema Fundamental do Cálculo para achar a derivada da função.
e)
Ver solução completaQuestão 72
Considere:
Onde é a função cujo gráfico é dado abaixo:
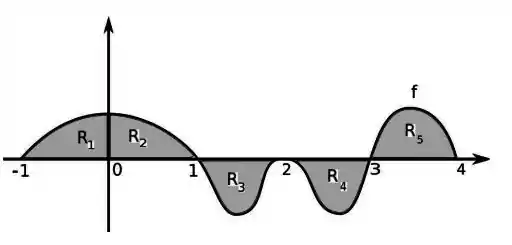
Sabendo que as áreas das regiões , , , e são:
, , , e .
Determine os intervalos de crescimento da função .
Ver solução completaQuestão 73
Seja
É dado que
- Determine
- Ache a área do triangulo limitado pelos eixos e pela reta tangente ao gráfico de no ponto .
Questão 75
-
Define a função onde f(x) é uma função definida por partes.
- Dê uma definição de por partes.
Questão 76
a. Seja contínua. Existe uma função com e ? Existe uma função com e ?
b. Seja derivável. Existe uma função com e
c. Existe derivável com ?
Ver solução completaQuestão 77
- Define a função onde f(x) é uma função definida por partes.
- Determine onde é diferenciável.
Questão 79
seja a taxa de consumo mundial de petróleo, em que é medido em anos começando em em janeiro de e é medida em barris por ano
- O que significa
Questão 81
Sejam e números reais e uma função diferenciável tal que , , e
O valor de
Ver solução completaQuestão 82
Utilizando o Teorema Fundamental do Cálculo, obtenha as seguintes integrais:
b)
Ver solução completaQuestão 83
Utilizando o Teorema Fundamental do Cálculo, obtenha as seguintes integrais:
e)
Ver solução completaQuestão 84
Utilizando o Teorema Fundamental do Cálculo, obtenha as seguintes integrais:
a)
Ver solução completaQuestão 86
Utilizando o Teorema Fundamental do Cálculo, obtenha as seguintes integrais:
d)
Ver solução completaQuestão 87
Utilizando o Teorema Fundamental do Cálculo, obtenha as seguintes integrais:
f)
Ver solução completaQuestão 88
Utilizando o Teorema Fundamental do Cálculo, obtenha as seguintes integrais:
g)
Ver solução completaQuestão 89
Calcule as integrais abaixo, utilizando para isso o Teorema Fundamental do Cálculo:
a)
Ver solução completaQuestão 90
Calcule as integrais abaixo, utilizando para isso o Teorema Fundamental do Cálculo:
b)
Ver solução completaQuestão 91
Utilizando o Teorema Fundamental do Cálculo, obtenha as seguintes integrais:
h)
Ver solução completaQuestão 93
Calcule as integrais abaixo, utilizando para isso o Teorema Fundamental do Cálculo:
c)
Ver solução completaQuestão 94
Calcule as integrais abaixo, utilizando para isso o Teorema Fundamental do Cálculo:
d)
Ver solução completaQuestão 95
Calcule as integrais abaixo, utilizando para isso o Teorema Fundamental do Cálculo:
e)
Ver solução completaQuestão 96
Calcule as integrais abaixo, utilizando para isso o Teorema Fundamental do Cálculo:
g)
Ver solução completaQuestão 97
Calcule as integrais abaixo, utilizando para isso o Teorema Fundamental do Cálculo:
i)
Ver solução completaQuestão 98
Calcule as derivadas das seguintes funções, utilizando para isso o Teorema Fundamental do Cálculo:
a)
Ver solução completaQuestão 99
Calcule as integrais abaixo, utilizando para isso o Teorema Fundamental do Cálculo:
e)
Ver solução completaQuestão 100
Calcule as integrais abaixo, utilizando para isso o Teorema Fundamental do Cálculo:
h)
Ver solução completaQuestão 101
Calcule as derivadas das seguintes funções, utilizando para isso o Teorema Fundamental do Cálculo:
b)
Ver solução completaQuestão 102
Calcule as derivadas das seguintes funções, utilizando para isso o Teorema Fundamental do Cálculo:
c)
Ver solução completaQuestão 103
Calcule as derivadas das seguintes funções, utilizando para isso o Teorema Fundamental do Cálculo:
f)
Ver solução completaQuestão 104
Calcule as derivadas das seguintes funções, utilizando para isso o Teorema Fundamental do Cálculo:
d)
Ver solução completaQuestão 105
Calcule as derivadas das seguintes funções, utilizando para isso o Teorema Fundamental do Cálculo:
e)
Ver solução completaQuestão 106
Use o Teorema Fundamental do Cálculo para calcular as derivadas das funções:
Ver solução completaQuestão 107
Use o Teorema Fundamental do Cálculo para calcular as derivadas das funções:
Ver solução completaQuestão 108
Use o Teorema Fundamental do Cálculo para calcular as derivadas das funções:
Ver solução completaQuestão 109
Use o Teorema Fundamental do Cálculo para calcular as derivadas das funções:
Ver solução completaQuestão 110
Use o Teorema Fundamental do Cálculo para calcular as derivadas das funções:
Ver solução completaQuestão 112
Use o Teorema Fundamental do Cálculo para calcular as derivadas das funções:
Ver solução completaQuestão 113
Use o Teorema Fundamental do Cálculo para calcular as derivadas das funções:
Ver solução completaQuestão 114
Use o Teorema Fundamental do Cálculo para calcular as derivadas das funções:
Ver solução completaQuestão 115
Use o Teorema Fundamental do Cálculo para calcular as derivadas das funções:
Ver solução completaQuestão 116
Use o Teorema Fundamental do Cálculo para calcular as derivadas das funções:
Ver solução completaQuestão 118
Use o Teorema Fundamental do Cálculo para calcular as derivadas das funções:
Ver solução completaQuestão 119
Use o Teorema Fundamental do Cálculo para calcular as derivadas das funções:
Ver solução completaQuestão 120
Utilizando o Teorema Fundamental do Cálculo, obtenha as seguintes integrais:
c)
Ver solução completaQuestão 121
Q01IV) Responda às perguntas abaixo no espaço adequado no seu caderno de respostas. As soluções devem ser sucintas e a resposta final deve estar destacada do restante da solução.
- Seja . Quanto vale ?
Questão 122
Se é contínua em , então o Teorema fundamental do Cálculo afirma que a derivada da função é igual a no intervalo . Vamos usar este resultado para calcular a derivada da função
- Verifique que, se e , então
- Use a regra da cadeia e o Teorema Fundamental do Cálculo para determinar
Questão 125
Em cada item, utilize o Primeiro Teorema Fundamental do Cálculo, propriedades da integral (se necessário) e as regras de derivação (se necessário) para calcular a derivada da função :
b)
Ver solução completaQuestão 126
Sejam e funções deriváveis e uma função contínua tais que:
Sabendo que , e , determine:
- e
- A equação da reta tangente ao gráfico de em
Questão 134
Mostre que o gráfico da função dada por
É parte de uma reta. Determine o coeficiente angular dessa reta.
Ver solução completaQuestão 135
Considere contínua. Decida se a proposição é falsa ou verdadeira.
Se
é crescente no intervalo , então é crescente no intervalo .
Ver solução completaQuestão 148
Em cada item, utilize o Primeiro Teorema Fundamental do Cálculo, propriedades da integral (se necessário) e as regras de derivação (se necessário) para calcular a derivada da função :
b)
Ver solução completaQuestão 150
Seja uma função contínua que satisfaz sendo uma constante não nula. O valor de é igual a:
- 2.
- 4.
- 6.
- 0.
- 1.
Questão 153
A taxa de gasto de combustível de um foguete em tempo é representada por e é obtida através da relação , onde é o gasto acumulado. Obtenha se for dada por:
Justifique todas as passagens.
Ver solução completaQuestão 158
Considere a função , , dada por:
Calcule , justificando todas as passagens.
Ver solução completaQuestão 165
Seja uma função contínua e considere definida por Sabendo que a reta tangente ao gráfico de no ponto tem equação o valor de ) é:
a)
b)
c)
d)
e)
Ver solução completaQuestão 167
Seja
Mostre que é uma função par
Calcule
Calcule a primeira derivada da função ,
Calcule
Determine a equação da reta tangente ao gráfico de em
Determine os pontos críticos de , e classifique cada um deles.
Ver solução completaQuestão 169
Se for uma função contínua tal que:
Para todo real ache uma fórmula explicita para .
Ver solução completaQuestão 176
Em cada item, utilize o Primeiro Teorema Fundamental do Cálculo, propriedades da integral (se necessário) e as regras de derivação (se necessário) para calcular a derivada da função :
b)
Ver solução completaQuestão 179
Determine a equação da reta tangente ao gráfico de no ponto , sendo:
Ver solução completaQuestão 182
Derivada de Funções dadas por Integral
Seja a função definida para por
Calcule a derivada de .
Ver solução completaQuestão 183
Derivada de Funções dadas por Integral
Use o 1º TFC para calcular a derivada da função
Ver solução completa
Questão 184
Derivada de Funções dadas por Integral
Considere a seguinte função
⋆ Calcule ;
⋆ Calcule .
Ver solução completa