Encontre os valores máximo e mínimo absolutos de
em .
Passo 1
E aí, tudo joia? Vamos dar uma olhada no gráfico dessa função pra ficar mais claro pra gente? Olha só:
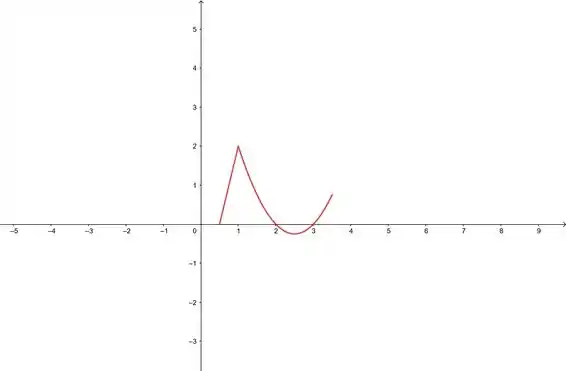
Vamos fazer isso algebricamente, e depois a gente só faz um check-up no gráfico, tá bom?
Passo 2
Olha só, a gente vai avaliar as duas expressões da função, como se fosse assim:
e
Vamos derivar cada parte dessa:
Essa derivada não zera, isso quer dizer que não tem como ter ponto de extremo nessa função além dos do intervalo. No caso a gente só analisa então o ...
Vamos ver a outra agora...
(derivamos...)
Isso vai zerar quando:
Vamos testar esses pontos agora e os pontos dos intervalos...
Passo 3
Ou seja, temos um ponto de máximo absoluto em e um de mínimo absoluto em .
Olhando no gráfico, a gente vê que isso confere, então prontinho😉
Resposta
Ponto mínimo:
Ponto máximo: